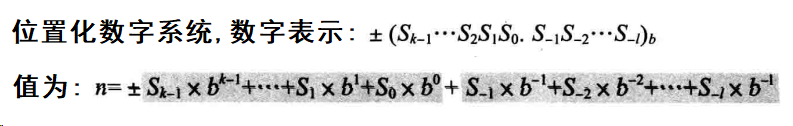[TOC]

计算机科学导论学习笔记

前言：当前作为一名IT互联网从业者，计算机技术日新月异，每天都有新概念、新技术的出现，而像我这样的万金油来说，越学到后面就越吃力，遇到瓶颈问题也随之增多，因为本身非科班出身，加之半路出家，针对于计算机基础知识掌握不牢或者说是不完整，所以我痛定思痛，下定决心重新学习计算机相关基础知识，从计算机科学导论，到计算机组成原理，到计算机网络、到操作系统，到数据结构，到程序算法、到应用开发、到安全运维开发。

今天 (2022年9月1日) 便从大神之路-起始篇,我们要站在巨人们的肩膀上，进行计算机科学导论的 学习，我将总结学习成果笔记，帮助后续入门学习的朋友。

随着现代计算机的发明，带来了新的学科，即计算机科学（简称计科）一词上一个非常广泛的概念，在此处我没将其定义为计算机相关的问题，现在计算机科学被划分成几个领域，总结归纳为两大类系统领域和应用领域.

• 系统领域：涵盖那些与硬件和软件构成直接有关的领域，例如计算机体系结构、计算机网络、安全问题、操作系统、算法、程序设计语言以及软件工程。
• 应用领域：涵盖了与计算机使用有关的领域，例如数据库、云物联和人工智能。

参考书籍:【计算机科学导论-第三版 （Foundations Of Computer Science - Third Edition) 】作者： [美] 贝赫鲁兹.佛罗赞 (Behrouz Forouzan) PS: 当下已经第四版了、

参考视频：【计算机导论】计算机科学导论（大神之路-起始篇）

---

第 2 部分 数据的表示和运算

描述：该部分包括第2、3和4章，我们分别进行如下学习。

• 第2章讨论了数字系统，数量如何能使用符号来表示。

• 第3章讨论了不同的数据如何存储在计算机中。

• 第4章讨论了一些基本的算术运算与位(逻辑)运算。

原文地址: https://mp.weixin.qq.com/s/RkQHKYM-b57CBlr553WZeg

2.数字系统

什么是数字系统?

用独特的符号（数码）来表示 一个数字 ， 在不同的系统中，一个数字有不同的表示方法，使用有限的数字符号来表示数字，所以数码需要重复使用。

例如，（2A)16和(52)8都是指同样的数量（42)10，但是他们的表示截然不同。

常见的数字系统，阿拉伯数字系统 （0-9），罗马数字系统 (I I I I I I IV V VI VII …..).

数字系统分类： 主要分为两类分部是位置化系统（主要讲解）和非位置化系统（简单提及）

2.1 位置化系统

在位置化数字系统中，数字中符号所占据的位置决定了其表示的值。

weiyigeek.top-位置化数字系统中

其中，S是一套符号集，b是底（或基数）等于S符号集中的符号总数，其中S1和Sk是代表分数部分或整个数字的符号，+、- 表示数字为正或者负。

2.2 进制系统转换

描述： 计算机由于其组成由成千上万个晶体管组成，通过其开/关完成或记录各项操作，则计算机只能识别 0 和 1，所以计算机底层识别通常是二进制的数据。

所以在讨论学习位置化数字系统前，我们需要针对各进制系统的表示与转换做一个学习（此基础知识非常重要）

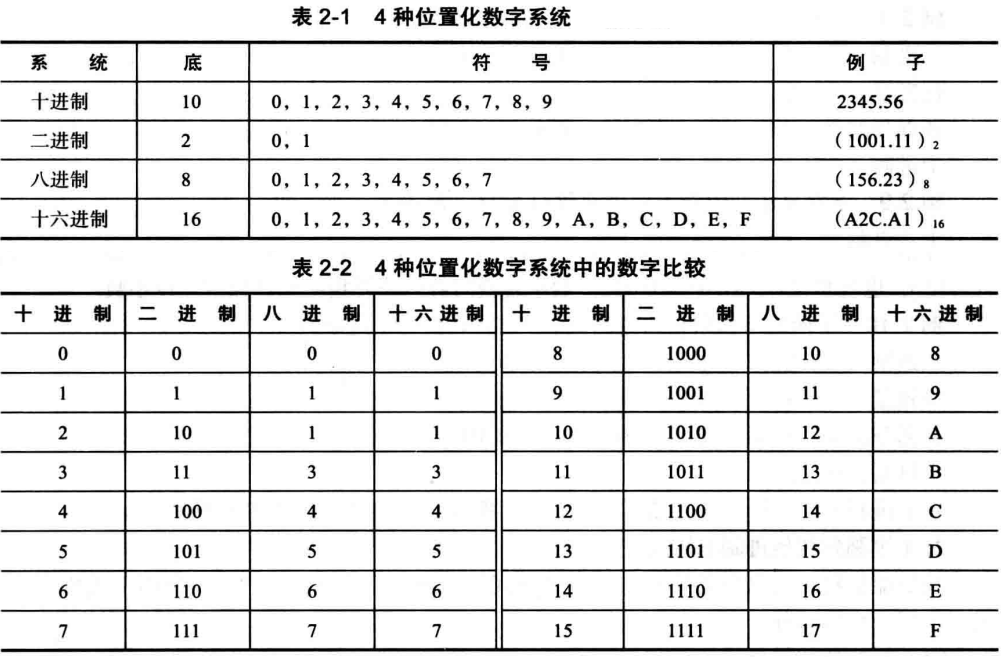
(1) R 进制系统的表示 （R 可为 二、八、十、十六）

描述：即在计算机数字系统常用进制系统是二进制 (Binary)、八进制(Octal)、十进制(Decimal)、十六进制(Hexadecimal)，其原则为逢R进一。

二进制（Binary）：源于拉丁词根bini（二），它只有 0 和 1 两个数表示，常用下标2或者B表示，例如：数值 3 的二进制表示为 (11)₂ 或者 11B，计算机中数据通常是以二进制模式(串)存储与计算机中执行.

八进制（Octal）：源于拉丁词octo (八)，由 0 ~ 7 八个数表示，常用下标8或者O表示，例如：数值 8 的八进制表示为 (10)₈ 或者 10O.

十进制（Decimal）：源于拉丁词 decem (十) ，由 0 ~ 9 十个数表示，常用下标10或D表示，例如：数值 10 的十进制表示为 (10)₁₀ 或者 10D ，该进制适合人类阅读理解.

十六进制（Hexadecimal）：源于希腊词根hex (六) 和 decem（十），由 0 ~ 9 A ~ E (分别等于 10~15) 十六个数表示，常用下标10或H表示，例如：数值 30 的十进制表示为 (1E)₁₆ 或者 1EH 。

此处以人类方便理解的十进制系统（以10为底）为例，进行讲解在整数、位置量、最大值、实数相关概念

• 整数：即没有小数部分的整型数字。
• 位置量：即用底（或者基数）的幂运算进行表示。例如，10的幂（10^0 , 10^1 , ~ , 10^(k-1)）
• 最大值：即使用数字K来表示十进制整数的最大值位数。例如，当k为5位时，其N_max = 10⁵ - 1 = 99 999
• 实数：即小数点后的部分数字，在十进制中小数点(.)是用于分割整数和小数部分的。

weiyigeek.top-整数、位置量、最大值、实数

十进制系统（以10为底）示例演示：

# 1.在十进制系统中，为了简便通常省略括号、底、以及正号(对于正数），例如 +(1024.1024)10, 写成 1024.1024 即可底号与加号是隐含的。

# 2.位置量，例如在十进制系统中使用位置量表示整数 +256.
位置量 10^2     10^1     10^0
数字   2        5        6
N =+  2*10^2 + 5*10^1 + 6*10^0  (值为256) 

# 例如，在十进制系统中使用位置量表示整数 -1024.
位置量 10^3     10^2     10^1     10^0
数字   1        0        2        4
N =- (1*10^3 + 0*10^2 + 2*10^1 + 4*10^0) (值为-1024) 

# 3.最大值，当k为数码数量为3时，其十进制系统整数最大值为 999
Nmax = 10^3 - 1 = 999

# 4.实数, 显示实数 +10.24 的位置量
位置量 10^1     10^0     10^-1     10^-2
数字   1        0     .  2        4
N =- 1*10^1 + 0*10^0 .  2*10^-1 + 4*10^-2 (值为10.24)

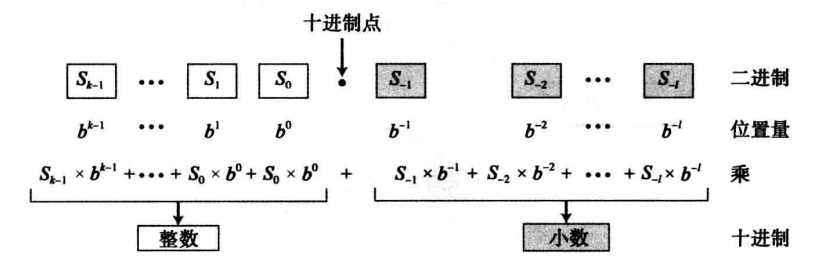
为了方便比较，此处再以计算机常用的二进制系统（以2为底）进行整数与实数进行讲解，可以如下图所示中得到计算的相关表达式，相比较于十进制只是将基数进行改变了，所以说八进制与十六进制的计算便不展开说明了。

weiyigeek.top-二进制

二进制系统（以2为底）示例演示：

# 1.位置量，例如在二进制系统数（1111）2等值于十进制数15.
位置量 2^3   2^2   2^1   2^0
数字   1     1     1     1
N =+  1*8 + 1*4 + 1*2 + 1*1  (相加十进制值为15) 

# 2.最大值，当k为数码数量为4时，其二进制系统整数最大值为 15
Nmax =  2^4 - 1 = 16 - 1 = 15

# 3.实数, 例如以下计算机与十进制5.75等值的二进制数（101.11）2
位置量 2^2    2^1     2^0     2^-1     2^-2
数字   1      0       1     . 1        1
R =+ 1*2^2 + 0*2^1 + 1*2^0 . 2*2^-1 + 2*2^-2 
R =+ 4 + 0 + 1 . 0.5 + 0.25 (值为5.75)

温馨提示: 计算机存储正负数的方式是不同的。（后续会有介绍）

(2) R 进制间相互转换

最常用的方式就是按权展开或者是 8421码快速进行进制的转换。

例如，将 （123）₁₀ 以按权方式展开。

123 = 100 + 20 + 3 = 1 * 10^2 + 2 * 10^1 + 3 * 10^0 (系数 * 基数 ^ 权) 相加即可
- 系数：每一位上的数据
- 基数（底）：X进制基数就是X，此的基数为 10
- 权：按从又右到左的顺序，从0开始编号，对应位上编号即为该位的权.

2.1 任意进制转换为十进制

其它进制转换为十进制是简单而迅速的，将数码乘以其在源系统中的位置量并求和便得到十进制中的数.

weiyigeek.top-任意进制转换为十进制

示例演示：

# 1.将二进制数（110.11）2 转换为十进制数 6.75。
二进制 1   1   0   . 1    1 
位置量 2^2 2^1 2^0   2^-1 2^-2 
N = 1*4 + 1*2 + 0*1 . 0.5 + 0.25 = 6.75

# 2.将八进制数(23.17)8转换为十进制数约 19.234
八进制 2   3   .  1    7
位置量 8^1 8^0 .  8^-1 8^-2 
N = 2*8^1 + 3*8^0 . 1/8 + 7/16 ≈ 19.234

# 3.将十六进制(1A.23)转换为十进制数约 26.137
十六进制  1    A   .  2     3
位置量   16^1 16^0 . 16^-1  16^-2
N = 1*16^1 + 10*16^0 . 2*16^-1 + 3*16^-2
N = 16 + 10 . 1/8 + 3/256 ≈ 26.137

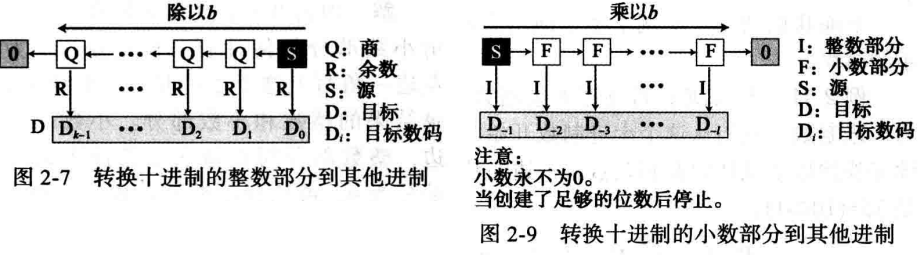
2.2 十进制转换为其他进制

将十进制转换到其他等值的其他进制，需要两个过程即整数部分和小数部分。

weiyigeek.top-十进制转换为其他进制

• 整数部分：在进行整数部分的转换可使用连除法。

例如，将 （58）₁₀ 转换为二进制的方法，此处采用除积倒取余（连除）法（也适于八进制、十六转换只是将连除的除数为基数），进行连除以2得到商和余数，当然日常使用8421码更为简单与二进制互换，此处主要讲解的是方式方法而已。

58 % 2 = 0  # 最低位
29 % 2 = 1
14 % 2 = 0
7 % 2  = 1
3 % 2  = 1
1 % 2  = 1  # 最高位 (有效位)
0
二进制的表示为 ：11 1010 (从下往上) ，而在八位寄存器通常表示为 0011 1010

• 小数部分：在进行小数部分的转换可使用连乘法，此处需要非常注意某些考试常常考带小数的转换。

# 1.将十进制的0.625转为二进制数结果为(0.101)2 ，注：此处由于没有整数部分，所以只演示小数部分
# 这里以2为底，将小数连乘以2并记录整数和小数部分，小数部分移到右边，而整数部分分别写在每次运算的下面，直到小小数部分为0，或者达到足够位数时结束。
十进制    0.625 *2       0.25(取小数部分)*2  0.50*2  0.00(连乘截止)
连乘结果  1.25            0.50              1.00
二进制    1(取整数部分)    0                 1       结果: (0.101)2


# 2.将十进制0.634转换为八进制且精确到4位小数。结果为 (0.5044)8
十进制   0.634*8  0.072*8  0.576*8  0.608*8  0.864(只取四位连乘截止)
连乘结果 5.072    0.576    4.608     4.864
八进制   5        0        4        4      结果: (0.5044)8


# 3.将十进制数178.6转换为十六进制且精确到1位小数，结果为 
十进制         0   11     178    . 0.6*16
连除.连乘结果       11/16  178/16 . 9.6  
十六进制            B     2(余数) . 9       结果: (B2.9)16

快速将十进制（通常小于256）为二进制数间的互相转换方法。

例如，将 （111010）₂ 转换为十进制的方法（位权 与 8421码），将展开的位权进行相加，其结果为 32 + 16 + 8 + 2 = (58)₁₀，应用此方法可以快速进行 十进制与二进制间的互换

描述: 上一个示例中讲解位权使用方法，这里在再讲讲8421码是BCD代码中最常用得一种，常用于二进制转十进制，此种编码方式中每一位二进制代码的1都是代表一个固定数值,把每一位1代表的十进制数加起来,所得的结果就是十进制。

二进制(八位寄存器)	0	0	1	1	1	0	1	0
位权(位置量)	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
按位权展开	0*(2^7)	0*(2^6)	1*(2^5)	1*(2^4)	1*(2^3)	0*(2^2)	1*(2^1)	0*(2^0)
8 4 2 1 码	0*128	0*64	32	16	8	0*4	2	0*1

例如，当分母是2的幂次时，用类似方法将十进制小数转为二进制数，计算机十进制数 27 / 64 转为二进制，其结果为 (0.011011)2。

位权(位置量)	2^-1	2^-2	2^-3	2^-4	2^5	2^6	2^-7	2^-8
按位权展开(十进制对等)	1/2	1/4	1/8	1/16	1/32	1/64	1/128	1/256
十进制 27 / 64	0	16/64	8/64	0	2/64	1/64	0	0
计算结果	0	1/4	1/8	0	1/32	1/64	0	0
转换结果	0	1	1	0	1	1	0	0

由上表可知，根据十进制对等的值排列这些分数，由于1/2 与 1/16缺失，我们使用了0代替，所以其二进制结果为 (0.011011)2

2.3 二进制转八进制、十六进制

我们能轻松将数字从二进制转换到八进制，反之亦然。这是因为在这两个底之间存在一种关系：二进制中的3位恰好是八进制中的1位。

例如，将（111010）₂ 转换为八进制方法： 从右往左起每逢三位二进制转1位八进制，当不足三位的在最左边添0补齐，反之八转二，每一位八进制转换为三位二进制位表示，其结果为（72)₈。

# 将（111010）划分位三位一组
111 010
7   2
# 结果为 (72)O

我们能轻松将数字从二进制转换到十六进制，反之亦然。这是因为在这两个底之间存在一种关系：二进制中的4位恰好是十六进制中的1位。

例如，将（111010）₂ 转换为十六进制方法： 从右往左起每逢四位二进制转1位十六进制，当不足四位的在最左边添0补齐，反之十六转二，每一位十六进制转换为四位二进制位表示，其结果为（31)₁₆。

# 将（111010）划分位四位一组不足以0想做向左补齐
0011 1010
3    A
# 结果为 (3A)H

温馨提示：如果需要将数字从八进制转换到十六进制，我们可以使用二进制系统作为临时中介系统。

2.4 数码的数量

在进行十进制转换为其他系统进制时我们可能需要知道数码的数量，我们可以通过 k=log_bN 的关系（k 是以b为底N的对数，N = b^k）进行计算，其 中b为基数(底数)、N为该数值的整数的十进制。

例如，我可以找到十进制数 234 转换为 2、8、10、16进制中所占的对应位数。

• 十进制 k= log₁₀234 = 2.37 = 3 位数
• 二进制 k= log₂234 = 7.8 = 8 位数，即 234 = (1110 1010)2
• 八进制 k= log₈234 = 2.62 = 3 位数 ，即 234 = (352)8
• 十六进制 k= log₁₆234 = 1.96 = 2 位数，即 234 = (EA)16

在从一个底装换为另外一个转换中，我们需要知道源系统数码的最大数量（b1^k-1, 其中b1是源数码基数，使用k个数码），意味着目标系统拥有的最大数是( b2^x - 1 ，其中 b2是目标数码基数，使用x个数码来装载源系统的值)，因此其关系是 b2^x - 1 ≥ b1^k-1 (b2^x ≥ b1^k )，其表达式为 x ≥ k * (logb1 / logb2) 。

例如，找出二进制（目标数码）数码最小数，用于存储一个最大的6个数的十进制数（源目标数码）。

即k=6, b1=10, b2=2 , 即 x = 6 （log10 / log2） = 6 ( 1 / 0.30103 ) = 20，即我们需要20位二进制数（1 048 575）来存放6位10进制数码最大值（999 999）。

---

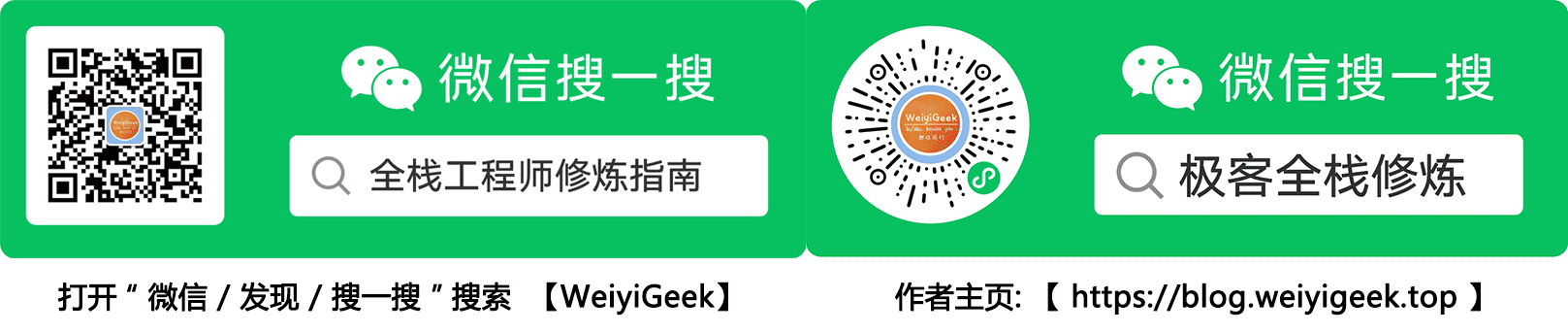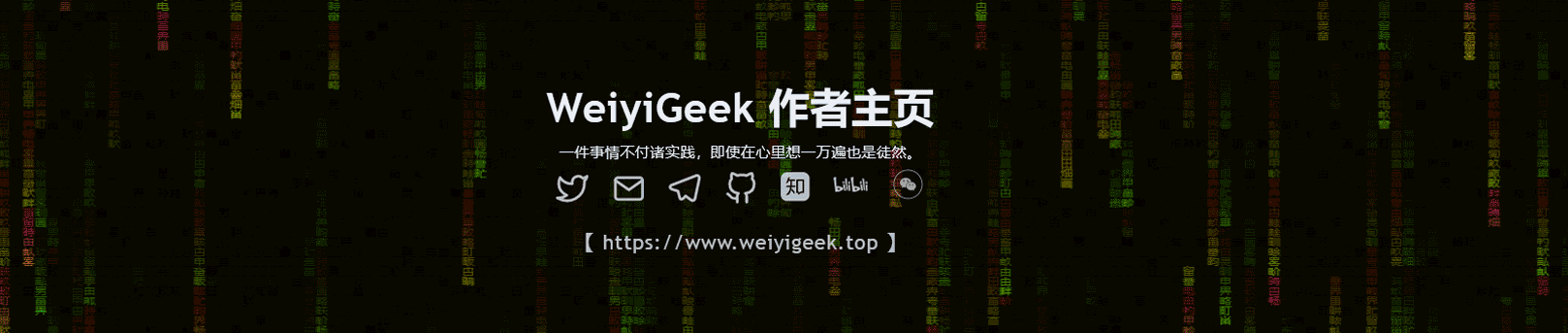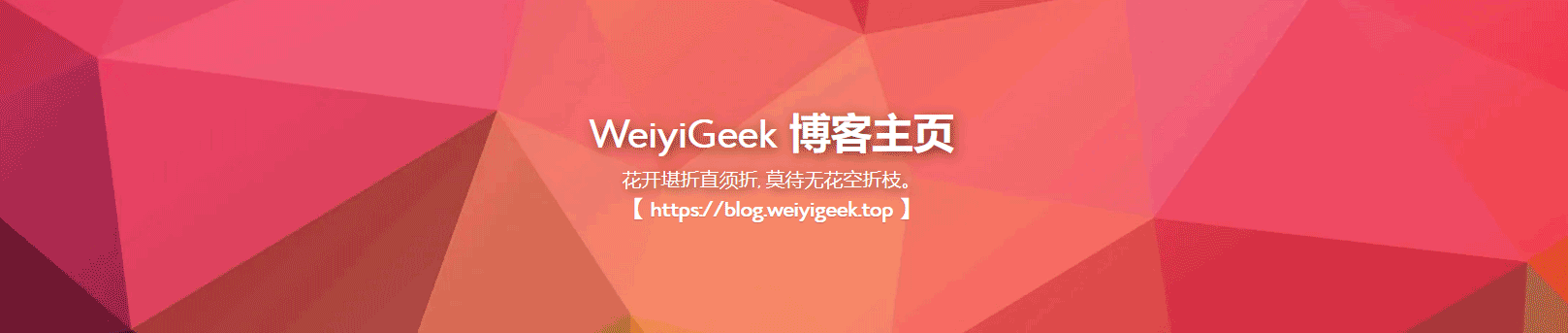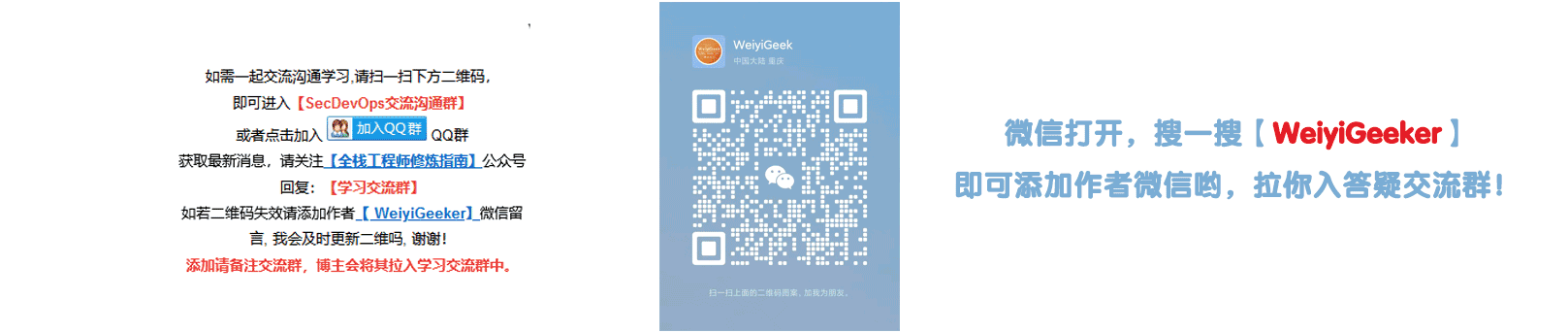
2.3 非位置化数字系统

非位置化数字系统仍然是使用有限的数字符号，每个符号对应一个值，其所在的位置通常与其值无关，因为每个符号值都是固定的。

为了求得该数字的值，可以把所有符号表示的值进行相加，但是需要遵循特定法则将符号值进行相加。

• 大值 ≥ 小值 ，其大值在前，小值在后是直接相加即可， 例如 VII = 5 + 1 + 1
• 大值＞小值 ，其小值在前，大值在后时用大值减去小值，例如 IV = 5 - 1
• 当 S1 ＞ 10 S2，则符号S2不能在符号S1之前，例如 I 和 V 不能在C之前，因为 100 ≥ 10 1 以及 100 ≥ 10 * 5.
• 当在6种符号（除I以外的所有符号）中的任意一个上方加横杠表示乘以1000，如下图所示
• 在罗马数字在其系统中缺少码0，尽管罗马人适用单词nulla表示零的概念。