[TOC]
计算机科学导论学习笔记 前言:当前作为一名IT互联网从业者,计算机技术日新月异,每天都有新概念、新技术的出现,而像我这样的万金油来说,越学到后面就越吃力,遇到瓶颈问题也随之增多,因为本身非科班出身,加之半路出家,针对于计算机基础知识掌握不牢或者说是不完整,所以我痛定思痛,下定决心重新学习计算机相关基础知识,从计算机科学导论,到计算机组成原理,到计算机网络、到操作系统,到数据结构,到程序算法、到应用开发、到安全运维开发。
今天 (2022年9月1日) 便从大神之路-起始篇,我们要站在巨人们的肩膀上,进行计算机科学导论的 学习,我将总结学习成果笔记,帮助后续入门学习的朋友。
随着现代计算机的发明,带来了新的学科,即计算机科学(简称计科)一词上一个非常广泛的概念,在此处我没将其定义为计算机相关的问题,现在计算机科学被划分成几个领域,总结归纳为两大类系统领域和应用领域.
系统领域:涵盖那些与硬件和软件构成直接有关的领域,例如计算机体系结构、计算机网络、安全问题、操作系统、算法、程序设计语言以及软件工程。
应用领域:涵盖了与计算机使用有关的领域,例如数据库、云物联和人工智能。
参考书籍:【计算机科学导论-第三版 (Foundations Of Computer Science - Third Edition) 】作者: [美] 贝赫鲁兹.佛罗赞 (Behrouz Forouzan) PS: 当下已经第四版了、
参考视频:【计算机导论】计算机科学导论(大神之路-起始篇)
第 2 部分 数据的表示和运算 描述:该部分包括第2 、3 和4 章,我们分别进行如下学习。
第2 章讨论了数字系统,数量如何能使用符号来表示。
第3 章讨论了不同的数据如何存储在计算机中。
第4 章讨论了一些基本的算术运算与位(逻辑)运算。
原文地址: https://mp.weixin.qq.com/s/XmsELA7atGCwDnfIP5yMtw
3.数据存储 描述:计算机是一个可编程的数据处理机器,在进行数据的存储学习前需要理解数据的特性。
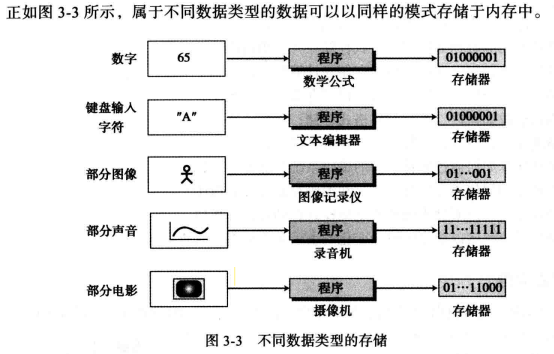
3.1 数据类型 如今,数据以不同形式出现,如数字、文本、音频、图像和视频,而在计算机中常常使用多媒体来定义包含它们。
在其计算机内部数据都是采用统一的数据表示法转换后存入计算机中(无需辨别它们表示的是何种数据类型),当数据需要从计算机输出时在还原回来,此种通用格式称为位模式。
位(bit, binary digit 缩写) : 存储在计算机中的最小单元,只有 0 或 1(电子开关),其代表设备的某一状态。
位模式: 使用其表示数据的不同类型,它是一个序列,有时被称为位流,通常长度为8的位模式被称为1字节,例如 16个位组成的位模式 1000 1010 1111 1111(需要16个电子开关)。
数据压缩:为了占用较少的(节约)内存空间,数据在存储到计算机之前通常需要被压缩。
错误检测和纠正:在传输和存储数据时,需要针对其数据进行错误检测和纠正。
3.2 数字存储 描述: 在存储到计算机内存中之前,数字被转换到二进制系统,对于整数的转换还是非常简单,而对于小数点,计算机使用两种不同的表示方法即定点 (把数字作为整数存储——没有小数部分) 和 浮点 (把数字作为实数存储——带有小数部分)。
本节讲解的重点,从计算机中有无符号位数的表示和存储、整数以及实数的表示和存储、到原码、反码、补码的介绍计算。
(1) 无/有符号数
寄存器的位数反映无符号数的表示范围
8 位 = 2^8 = 1111 1111 (二进制) = 0 ~ 255
16 位 = 2^16 = 1111 1111 1111 1111 (二进制) = 0 ~ 65535
符号表示格式:
真值数:带符号的数,即带“+”或“-”符号的数为真值。
机器数:符号数字化的数, 即用0,1这种表示正负的数称为机器数。
例如:下表中带符号的数与符号数字化的数分别对应,利用符号加绝对值表示法.
带符号的数
符号数字化的数
+ 0.1011
0(.)1011
- 0.1011
1(.)1011
+ 1100
0 1100(.)
- 1100
1 1100(.)
温馨提示:从上之中我们可以看到计算机中是如何存储负数的,在其值的最高位为符号标志位,其余的为数值位。
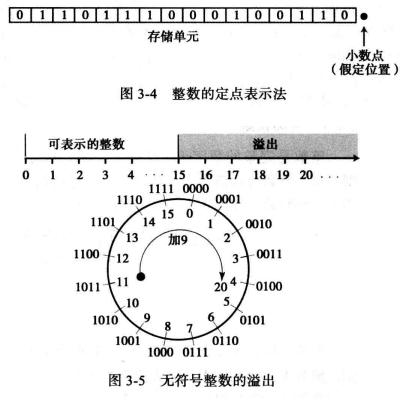
(2) 整数的存储 整数是完整的数字(即没有小数部分),通常使用定点表示法(此种表示法中,小数点是假定的,但并不存储)存储在内存中,整数可以被当作小数点位置固定的数字,小数点固定在最右边。
为了更有效地利用计算机内存,无符号和有符号的整数在计算机中存储方式是不同的,即分为下面三种方法
无符号表示法: 其只包括零和正数的非负整数,它的范围介于0到无穷大之间,该方法可以提高存储的效率。
1.存储无符号整数:首先将整数变成二进制数,如果二进制位数不足n位,则在二进制数的左边补0,使它的总位数为n位,如果位数大于n,该整数无法存储,导致溢出的情况发生,我们后面要讨论。
例如,将 7 存储在 8 位存储单元中,使用符号表示法
计数:当我们计数时,不需要负数。可以从1 (有时0)开始增长。
寻址:有些计算机语言,在一个存储单元中存储了另一个存储单元的地址。地址都是从0 (存储器的第一个字节)开始到整个存储器的总字节数的正数,在这里同样也不需要用到负数。因此无符号整数可以轻松地完成这个工作。
存储其他数据类型:我们后面将谈到的其他数据类型(文本、图像、音频和视频)是以位模式存储的,可以翻译为无符号整数。
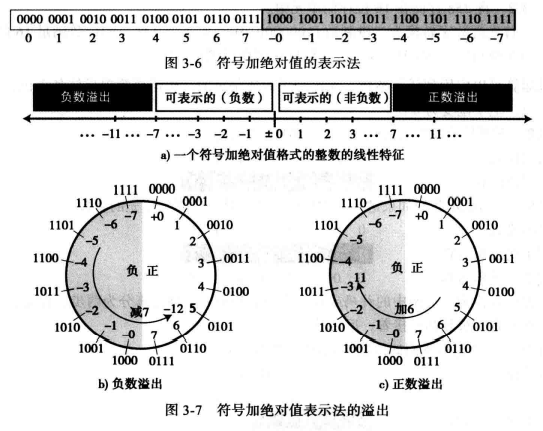
符号加绝对值表示法: 在存储整数中该方法并不常用,但该格式用于在计算机中存储部分实数,用符号加绝对值格式存储一个整数,需要用1个二进制位表示符号(0表示正,1表示负), 意味着在一个8 位存储单元中,可以仅用7 位表示数字的绝对值(不带符号)。因此,最大的正数值仅是无符号最大数的一半。在n位单元可存储的数字范围是 -(2^(n-1)-1) 至 +(2^(n-1)-1).
1.存储有符号整数: 最左位用于定义整数的符号(0表示正整数,1表示负整数)
例如,使用符号加绝对值表示法将+28与-28分别存储在8位存储单元中。
+28 = + (11100)2 = 0001 1100
-28 = - (11100)2 = 1000 1100
2.符号加绝对值表示法的溢出:同无符号整数一样,有符号的整数也会溢出,并且可能有正负两种溢出情况。
例如,当使用4位内存单元存储一个用符号加绝对值表示法的整数时出现的正负两种溢出,当我们试图存储一个比7大的正整数时,出现正溢出。
3.符号加绝对值表示法的应用:符号加绝对值表示法不用于存储整数,而用于存储部分实数,我们后面会看到,此表示法通常用于釆样模拟信号,例如,音频。
二进制补码表示法: 几乎所有的计算机都使用二进制补码表示法来存储位于n位存储单元中的有符号整数,例如,如果n 是4, 该范围是0000 到1111 ,这个范围分为两半:0000 到0110 以及1000 到1111 ,这两半按照左负右正的常规互相交换。赋值给负和非负(零和正)整数的位模式,即我们后续需要学习计算机基础的原码、反码、补码的相关知识(此处先不展开讲解)。
(3) 实数的存储 实数是带有整数部分和小数部分的数字,对于小数点的处理计算机适用定点和浮点 两种不同的表示方法。
定点表示法: 小数点按约定方式标出,但是尽管固定小数点的表示法(定点)可用于表示实数,但结果不一定精确或达不到需要的精度,所以带有很大的整数部分或很小的小数部分的实数不应该用定点表示法存储。
例如,在十进制系统中,假定我们用一种小数点右边2个数码,左边14个数码,总共16个数码的定点表示法。那么如果试图表示十进制数1.002 34,该系统的实数精度就会受损,该系统会把这个数字存储为1.00.
浮点表示法: 用于维持正确度或精度的解决方法,其允许小数点浮动,即可以在小数点的左右有不同数量的数码,此种方法极大地增加了可存储的实数范围,所以该方法适用于表示带有很大的整数部分或很小的小数部分的实数。
在浮点表示法中,无论十进制还是二进制,一个数字都由3部分组成,即 符号、位移量、定点数三部分。
第一部分是符号,可正可负。
第二部分是位移量,显示小数点应该左右移动构成实际数字的位移量。
第三部分是定点数,小数点位置固定的定点表示法。
在称作科学计数法(浮点表示法)的表示法中, 定点部分在小数点左边只有1 个数码而且位移量是10 的幂次。
例如,使用科学计数法表示十进制数 7 425 000 000 000 000 000 000
[TOC]
计算机科学导论学习笔记 前言:当前作为一名IT互联网从业者,计算机技术日新月异,每天都有新概念、新技术的出现,而像我这样的万金油来说,越学到后面就越吃力,遇到瓶颈问题也随之增多,因为本身非科班出身,加之半路出家,针对于计算机基础知识掌握不牢或者说是不完整,所以我痛定思痛,下定决心重新学习计算机相关基础知识,从计算机科学导论,到计算机组成原理,到计算机网络、到操作系统,到数据结构,到程序算法、到应用开发、到安全运维开发。
今天 (2022年9月1日) 便从大神之路-起始篇,我们要站在巨人们的肩膀上,进行计算机科学导论的 学习,我将总结学习成果笔记,帮助后续入门学习的朋友。
随着现代计算机的发明,带来了新的学科,即计算机科学(简称计科)一词上一个非常广泛的概念,在此处我没将其定义为计算机相关的问题,现在计算机科学被划分成几个领域,总结归纳为两大类系统领域和应用领域.
系统领域:涵盖那些与硬件和软件构成直接有关的领域,例如计算机体系结构、计算机网络、安全问题、操作系统、算法、程序设计语言以及软件工程。
应用领域:涵盖了与计算机使用有关的领域,例如数据库、云物联和人工智能。
参考书籍:【计算机科学导论-第三版 (Foundations Of Computer Science - Third Edition) 】作者: [美] 贝赫鲁兹.佛罗赞 (Behrouz Forouzan) PS: 当下已经第四版了、
参考视频:【计算机导论】计算机科学导论(大神之路-起始篇)
第 2 部分 数据的表示和运算 描述:该部分包括第2 、3 和4 章,我们分别进行如下学习。
第2 章讨论了数字系统,数量如何能使用符号来表示。
第3 章讨论了不同的数据如何存储在计算机中。
第4 章讨论了一些基本的算术运算与位(逻辑)运算。
原文地址: https://mp.weixin.qq.com/s/XmsELA7atGCwDnfIP5yMtw
3.数据存储 描述:计算机是一个可编程的数据处理机器,在进行数据的存储学习前需要理解数据的特性。
3.1 数据类型 如今,数据以不同形式出现,如数字、文本、音频、图像和视频,而在计算机中常常使用多媒体来定义包含它们。
在其计算机内部数据都是采用统一的数据表示法转换后存入计算机中(无需辨别它们表示的是何种数据类型),当数据需要从计算机输出时在还原回来,此种通用格式称为位模式。
位(bit, binary digit 缩写) : 存储在计算机中的最小单元,只有 0 或 1(电子开关),其代表设备的某一状态。
位模式: 使用其表示数据的不同类型,它是一个序列,有时被称为位流,通常长度为8的位模式被称为1字节,例如 16个位组成的位模式 1000 1010 1111 1111(需要16个电子开关)。
数据压缩:为了占用较少的(节约)内存空间,数据在存储到计算机之前通常需要被压缩。
错误检测和纠正:在传输和存储数据时,需要针对其数据进行错误检测和纠正。
3.2 数字存储 描述: 在存储到计算机内存中之前,数字被转换到二进制系统,对于整数的转换还是非常简单,而对于小数点,计算机使用两种不同的表示方法即定点 (把数字作为整数存储——没有小数部分) 和 浮点 (把数字作为实数存储——带有小数部分)。
本节讲解的重点,从计算机中有无符号位数的表示和存储、整数以及实数的表示和存储、到原码、反码、补码的介绍计算。
(1) 无/有符号数
寄存器的位数反映无符号数的表示范围
8 位 = 2^8 = 1111 1111 (二进制) = 0 ~ 255
16 位 = 2^16 = 1111 1111 1111 1111 (二进制) = 0 ~ 65535
符号表示格式:
真值数:带符号的数,即带“+”或“-”符号的数为真值。
机器数:符号数字化的数, 即用0,1这种表示正负的数称为机器数。
例如:下表中带符号的数与符号数字化的数分别对应,利用符号加绝对值表示法.
带符号的数
符号数字化的数
+ 0.1011
0(.)1011
- 0.1011
1(.)1011
+ 1100
0 1100(.)
- 1100
1 1100(.)
温馨提示:从上之中我们可以看到计算机中是如何存储负数的,在其值的最高位为符号标志位,其余的为数值位。
(2) 整数的存储 整数是完整的数字(即没有小数部分),通常使用定点表示法(此种表示法中,小数点是假定的,但并不存储)存储在内存中,整数可以被当作小数点位置固定的数字,小数点固定在最右边。
为了更有效地利用计算机内存,无符号和有符号的整数在计算机中存储方式是不同的,即分为下面三种方法
无符号表示法: 其只包括零和正数的非负整数,它的范围介于0到无穷大之间,该方法可以提高存储的效率。
1.存储无符号整数:首先将整数变成二进制数,如果二进制位数不足n位,则在二进制数的左边补0,使它的总位数为n位,如果位数大于n,该整数无法存储,导致溢出的情况发生,我们后面要讨论。
例如,将 7 存储在 8 位存储单元中,使用符号表示法
计数:当我们计数时,不需要负数。可以从1 (有时0)开始增长。
寻址:有些计算机语言,在一个存储单元中存储了另一个存储单元的地址。地址都是从0 (存储器的第一个字节)开始到整个存储器的总字节数的正数,在这里同样也不需要用到负数。因此无符号整数可以轻松地完成这个工作。
存储其他数据类型:我们后面将谈到的其他数据类型(文本、图像、音频和视频)是以位模式存储的,可以翻译为无符号整数。
符号加绝对值表示法: 在存储整数中该方法并不常用,但该格式用于在计算机中存储部分实数,用符号加绝对值格式存储一个整数,需要用1个二进制位表示符号(0表示正,1表示负), 意味着在一个8 位存储单元中,可以仅用7 位表示数字的绝对值(不带符号)。因此,最大的正数值仅是无符号最大数的一半。在n位单元可存储的数字范围是 -(2^(n-1)-1) 至 +(2^(n-1)-1).
1.存储有符号整数: 最左位用于定义整数的符号(0表示正整数,1表示负整数)
例如,使用符号加绝对值表示法将+28与-28分别存储在8位存储单元中。
+28 = + (11100)2 = 0001 1100
-28 = - (11100)2 = 1000 1100
2.符号加绝对值表示法的溢出:同无符号整数一样,有符号的整数也会溢出,并且可能有正负两种溢出情况。
例如,当使用4位内存单元存储一个用符号加绝对值表示法的整数时出现的正负两种溢出,当我们试图存储一个比7大的正整数时,出现正溢出。
3.符号加绝对值表示法的应用:符号加绝对值表示法不用于存储整数,而用于存储部分实数,我们后面会看到,此表示法通常用于釆样模拟信号,例如,音频。
二进制补码表示法: 几乎所有的计算机都使用二进制补码表示法来存储位于n位存储单元中的有符号整数,例如,如果n 是4, 该范围是0000 到1111 ,这个范围分为两半:0000 到0110 以及1000 到1111 ,这两半按照左负右正的常规互相交换。赋值给负和非负(零和正)整数的位模式,即我们后续需要学习计算机基础的原码、反码、补码的相关知识(此处先不展开讲解)。
(3) 实数的存储 实数是带有整数部分和小数部分的数字,对于小数点的处理计算机适用定点和浮点 两种不同的表示方法。
定点表示法: 小数点按约定方式标出,但是尽管固定小数点的表示法(定点)可用于表示实数,但结果不一定精确或达不到需要的精度,所以带有很大的整数部分或很小的小数部分的实数不应该用定点表示法存储。
例如,在十进制系统中,假定我们用一种小数点右边2个数码,左边14个数码,总共16个数码的定点表示法。那么如果试图表示十进制数1.002 34,该系统的实数精度就会受损,该系统会把这个数字存储为1.00.
浮点表示法: 用于维持正确度或精度的解决方法,其允许小数点浮动,即可以在小数点的左右有不同数量的数码,此种方法极大地增加了可存储的实数范围,所以该方法适用于表示带有很大的整数部分或很小的小数部分的实数。
在浮点表示法中,无论十进制还是二进制,一个数字都由3部分组成,即 符号、位移量、定点数三部分。
第一部分是符号,可正可负。
第二部分是位移量,显示小数点应该左右移动构成实际数字的位移量。
第三部分是定点数,小数点位置固定的定点表示法。
在称作科学计数法(浮点表示法)的表示法中, 定点部分在小数点左边只有1 个数码而且位移量是10 的幂次。
例如,使用科学计数法表示十进制数 7 425 000 000 000 000 000 000
1 2 3 十进制数:+ 7 425 000 000 000 000 000 000 科学计数法:7.425 x 10^21 (或者 +4.425E21)
例如,使用科学计数法表示数字 -0.000 000 000 000 023 2
1 2 3 十进制数: - 0.000 000 000 000 023 2 科学计数法: - 2.32 x 10^-14 (或者 - 2.32E-14)
例如,使用浮点格式(浮点表示法)表示数字-(0.00000000000000101)2
1 2 3 # 同样,小数左边只留一个非零数码,注意指数作为负的二进制数存储在计算机中。 二进制数:-(0.0 0000 0000 0000 0101)2 科学计数法: - 1.01 x 2^-14
规范化 :为了统一表示法固定部分,科学计数法(用于十进制)和浮点表示法(用于二进制)都在小数点左边适用唯一非零(0)数码。
例如,十进制系统中的数码可能是1~9,而二进制系统中该数码是1。即
1 2 十进制: ± d.xxxxxxxxxxx 其中, d 取值范围 1-9,x 取值范围 0-9 二进制: ± 1.yyyyyyyyyyy 其中, y 取值范围是 0 或 1 。
符号、指数和尾数 : 在一个二进制数规范化之后,只存储了一个数的三部分信息:符号、指数和尾数(小数点右边的位)
符号: 一个数的符号可以用一个二进制位来存储(0 或1 )。
指数(2的幂): 定义为小数点移动的位数,注意幂可以为正也可以为负。余码表示法(后面讨论)是用来存储指数位的方法。
尾数:是指小数点右边的二进制数,它定义了该数的精度,尾数是作为无符号整数存储的。
1 2 3 4 符号 指数 尾数 + 2^6 1.0001110101 + 6 0001110101
温馨提示: 小数点和定点部分左边的位1并没有存储(即1.),它们是隐含的
温馨提示:尾数是带符号的小数部分,像以符号加绝对值表示法存储的整数那样对待。
余码系统 : 正的和负的整数都可以作为无符号数存储,则在余码系统中的所有整数都是正数。而为了表示正的或负的整数,一个正整数(称为一个偏移量)加到每个数字中,将它们统一移到非负的一边,其中偏移量的值计算表达式 2^(m-1)-1, m 是内存单元存储指数的大小。
例如,对于4 位存储单元,则其偏移量是 2^(4-1)-1=7。
例如,我们可以用4 位存储单元在数字系统中表示16 个整数。使用一个单元作为0, 分开其他15 个(不等地)我们可以在-7〜8 的范围中表示整数,如图下图所示。在该范围中增加7 个单位到每个整数中,可以统一把所有整数向右移,使其均为整数而无需改变这些整数的相对位置,避免了相互调整,如图下图所示,新系统称为余7, 或者偏移量为7 的偏移表示法
IEEE 存储浮点数的标准
IEEE 是电气和电子工程师协会,定义了几种存储浮点数的标准,其中耳熟能详的有单精度和双精度
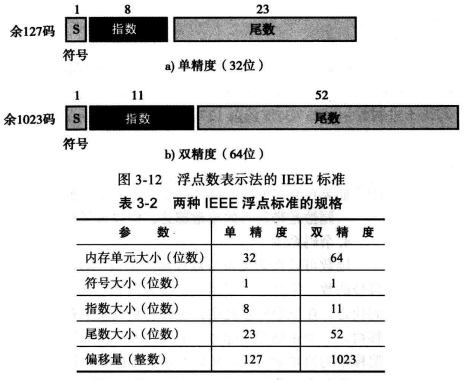
单精度数格式: 采用总共32 位来存储一个浮点表示法的实数。符号占用1 位(0 为正,1 为负),指数占用8 位(使用偏移量127 ),尾数使用23 位(无符号数)。该标准有时称为余127 码(Excess_127 ),因为偏移量是127 。
双精度数格式: 釆用总共64 位来存储一个浮点表示法的实数。符号占用1 位(0 为正,1 为负),指数占用11 位(使用偏移量1023 ), 尾数使用52 位。该标准有时称为余1023 码(Excess_1023 ), 因为偏移量是1023 。
IEEE 标准浮点数的存储
将一个实数可以存储为IEEE标准浮点数格式的步骤如下:
步骤 1.在S中存储符号(0或1 )。
例如,十进制5.75余127码(单精度)表示法。
1 2 3 4 5 6 符号 + S=0 二进制: 5.75 => 101.11 (小数点后连乘法) 规范化: + (1.0111)2 x 10^2 E和M值: E = 指数 + 余码 = 2 + 127 = 129 = (10000001)2, M = 尾数 = (0111)2 = 0111 000 ... 000 (在M右侧增加19个0使之成为23位) 表示法: S E M 存储数据: 0 10000001 0111 0000 0000 0000 0000 000
例如,十进制-0.0234375余127码(单精度)表示法。
1 2 3 4 5 6 符号: - S=1 二进制: 0.0234375 = 0.0000011 规范化: - (1.1)*10^-6 E和M值: E = 指数 + 余码 = -6 + 127 = 121 = (01111001)2, M = 尾数 = (1)2 = 1000 .... 0000 (在M右侧增加22个0使之成为23位) 表示法: S E M 存储数据: 1 01111001 1000 0000 0000 0000 0000 000
IEEE 标准存储的浮点数还原
将一个被IEEE标准存储的浮点数还原为原数字的流程如下:
步骤 1)找到S、E和M的值。
例如,将位模式(11001010000000000111000100001111)2以余127码的格式存储与内存中,请求该数字原本的十进制数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 S E M 1 10010100 00000000111000100001111 S = 1 , 则符号为负号(-) E = (10010100)2 - 127 = 148 - 127 = 21 (1.00000000111000100001111)2 x 2^21 (1000000001110001000011.11)2 -2 104 378.75
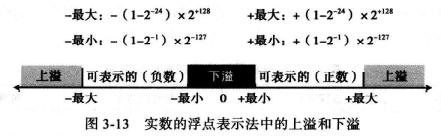
上溢和下溢
对于浮点数,有上溢和下溢两种情况,例如使用32 位内存单元(余127 码)的浮点表示法,该表示法不能存储很小或很大的绝对值。
如果试图存储绝对值很小的数导致下溢的情况。
如果试图存储绝对值很大的数导致上溢的情况。
零值存储 : 当有整数部分和小数部分的实数设置为零的时候是0.0 时,此时约定在这种情况下符号、指数和尾数都设为零。
截断错误 : 当使用浮点表示法存储实数时存储数字的值可能不是我们希望的。例如,假定我们需要在内存中用余
127 码表示法存储这个数字:
weiyigeek.top-截断错误
由上图可知小数部分右边的3 个1 被截掉了,这种原始数字与还原后数字的差异称为截断错误。在使用很小或很大数字的地方,如宇航业的计算中,这种类型的错误是很严重的。这种情况下, 我们需要更大的内存单元 (例如,64位,双精度) 和 其他的表示法。为此IEEE 定义了用于更大尾数的其他表示法。
(4) 原码、反码、补码定义计算 描述:说到计算机数据的表示和存储,不得不提到原码、反码、补码。
原码:二进制定点表示法, 即最高位为符号位 0 表示正, 1 表示负, 其余位表示数值位大小,比如 (0 000 0111) B= 7 而 (1 000 0111) B = -7
反码:正数的反码与其原码相同, 负数的反码时对其原码逐位取反(符号位除外)
补码:正数的补码与其原码相同, 负数的补码是在其反码的末尾加1,或者在原码减1在取反也是可以的(计算机中通常是使用补码来存放负数的)。
计算机中的原码、反码和补码快速计算了解(重点):
[八位寄存器]
数值 1
数值 -1
数值 1 +(-1)= 0
原码 0 000 0001
1 000 0001 (符号位为 1)
1 000 0010 = (0 000 0001 + 1 000 0001) = -2
反码 0 000 0001
1 111 1110 (符号位不变,按位取反)
1 111 1111 = (0 000 0001 + 1 111 1110) = - 0
补码 0 000 0001
1 111 1111 (反码+1)
0 000 0000 = (1111 1111 + 0000 0001) = 1 0000 0000 (八位寄存器取只取后八位)
温馨提示:
原码在表示数字0时,有两种方式表达 (0000 0000)B = 0 与 (1000 0000)B = -0,所以显然使用原码来表示数值正负不合适。
反码在表示数字0时,也有两种方式表达 (0000 0000)B = 0 与 (1111 1111)B = -0,所以显然使用反码来表示数值正负也是不合适。
补码在进行计算0时,可以在数值位减1再取反或者在数值位取反后再加1也是可以的,其结果表示是精确的,所以显然使用反码来表示数值正负是非常合适的,并且计算机默认是使用补码来表示数值的(重点)。
温馨提示:如果将符号位 与 数值位 在运行时进行对其分离,但是这样做会增加ACC累加器设计开销过大。
举例,求数值 7 与 - 7 的原码、反码、补码的二进制表示(八位寄存器)。
1 2 3 4 数值 7 | 数值 -7 原码 0 000 0111 | 1 000 0111 反码 0 000 0111 | 1 111 1000 补码 0 000 0111 | 1 111 1001
计算机中的原码、反码和补码取值范围:
定点整数
定点小数
原码 -(2^(n-1) - 1) ~ 2^(n-1) - 1
-1 < x < 1
反码 -(2^(n-1) - 1) ~ 2^(n-1) - 1
-1 < x < 1
补码 -2^(n-1) ~ 2^(n-1) - 1
-1 <= x < 1
温馨提示:定点小数精确的表示范围应该是,原码为 -1 * (1 - 2^-(N-1)) ~ 1 - 2^-(N-1) ,其补码为-1 ~ 1 - 2^-(N-1).
原码表示法公式(原理)
$$
$$
整数原码计算示例:如 15 与 - 15 数的表示流程。
数值 = 15 -> x = + 1111 -> [x]原 = 0,1111
小数原码计算示例:例如 0.15 与 - 0.15 数的表示流程。
数值 = 0.15 -> x = + 0.1111 -> [x]原 = 0.1111
原码特点: 表示简单直观但是在使用原码做加法时,会出现结果符号可正可负的问题。
正数的原码符号位为0;数值位为其真值 负数的原码符号位为1;数值位为其真值
补码表示法公式(原理)
$$
$$
整数补码计算示例:如 15 与 - 15 数的表示流程。
数值 = 15 -> x =1111 -> [x]补 = 0,1111
正数的补码符号位为0;数值位为其真值 负数的补码符号位为1;数值位为其真值对应位求反后末位加1
反码表示法公式(原理)
$$
$$
整数反码计算示例:如 15 与 - 15 数的表示流程。
数值 = 15 -> x = + 1111 -> [x]反 = 0,1111
小数反码计算示例:求 - 13 / 64 的反码
-(8 + 4 + 1) / 64 = - ( 1/8 + 1/16 + 1/64) = -(2^3 + 2^4 + 2^6) = - (0.001101)2 = 1.110010 (反码)
解释:1/8 = 2^-3 化为2进制为 (0.001)2 ,1/16 = 2^-4 化为2进制为(0.0001)2 ,1/64= 2^-6 化为2进制为 (0.000001)2
正数的补码符号位为0;数值位为其真值 负数的补码符号位为1;数值位为其真值对应位求反
移码表示法公式(原理)
计算步骤:
方法一(简单):在补码的基础上,符号位取反
方法二:[e]移 = 2^k + e , -2^k <= e <= 2^k
整数移码计算示例:如 9 与 - 9 数的表示流程。
x = + ( 1001 )2 , [x]补 = ( 0 1001 )2,[x]移 = ( 1 1001 )2
x = - ( 1001 )2 , [x]反 = ( 1 0110 )2,[x]补 = ( 1 0111 )2,[x]移 = ( 0 0111 )2
举例,求 - 13 / 64 的补码
-13/64=(-0.001101)2,[x]反=1.110010 ,[x]补=1.110011 ,[x]移=0.110011
有整数和小数部分组合形成的数值
描述:十进制数转换为任意进制数 , 通常采用基数相乘法,对整数部分用除基取余法,对小数部分用乘基取整法,最后将整数和小数拼接在一起。
例如,将十进制数123.6875转换成二进制数,最终结果为 (1111011.1011)2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 123 % 2 = 1 61 % 2 = 1 30 % 2 = 0 15 % 2 = 1 7 % 2 = 1 3 % 2 = 1 1 % 2 = 1 0.6875 * 2 = 1 = 1.3750 0.3750 * 2 = 0 = 0.7500 0.7500 * 2 = 1 = 1.5000 0.5000 * 2 = 1 = 1.0000
温馨提示:小数和整数不一样,整数可以连续表示,但小数是离散的。二进制的小数只能表示 1/2, 1/4, ……, 1/2n, 因此无法表示所有的十进制小数。
而在将整数和小数转换成为八进制或者十二进制时,在转换时应以小数点为界。
整数部分:在从小数点开始往左数,将一串二进制数分为3位(八进制)一组或4位(十六进制)一组,在数的最左边可根据需要加“0”补齐;(左补齐)
小数部分,从小数点开始往右数,也将一串二进制分为3位一组或4位一组,在数的最右边也可以根据需要加“0”补齐。(右补齐)
最终使总的位数为3或4的整数倍,然后分别用对应的八进制数或十六进制数取代;
例: 将二进制数 1111000010.01101 分别转换为八进制数和十六进制数。
1 2 3 4 5 6 [00]1 111 000 010.011 01[0] 1 7 0 2 3 2 => (1702.32)O [00]11 1100 0010.0110 1[000] 3 C 2 6 8 => (3C2.68)H
三种机器数小结
最高位为符号位,书写上用,(整数)或.(小数)将数值部分和符号位隔开。
对于正数,原码=补码=反码。
对于负数,符号位为1,其数值部分原码除符号位外每位按位取反末尾加1就为补码,如果不加一就为反码。
计算机里一般使用补码表示负数,例如,数值-15的二进制数为 1111 0001(8位寄存器)。
[y]补 连同符号在内,每位取反,末位加1,即得 [-y] 补,例如 -5 的补码为 1111 1011 (8位寄存器)。
如下图所显示无符号、符号绝对值、二进制补码等表示法的对比,例如,使用4位存储单元以存储0〜15 之间的无符号整数, 存储单元可以存储-8〜+7 之间的二进制补码整数。
3.3 文字存储 在任何语言中,文本的片断是用来表示该语言中某个意思的一系列的符号,而在计算机中可以用位模式来表示任何一个符号,例如
使用26个符号(A, B, C,…,Z)来表示大写字母
使用26个符号(a, b, c, •••, z)表示小写字母,
使用10个符号(0, 1, 2,…,9)来表示数字字符(不是实际的数字,后面将看到它们的不同之处)
使用单个符号(.,?,:,;,...,!)来表示标点。
使用特殊符号(如空格、换行和制表符)被用于文本的对齐和可读性。
在一种语言中,位模式到底需要多少位来表示一个符号?
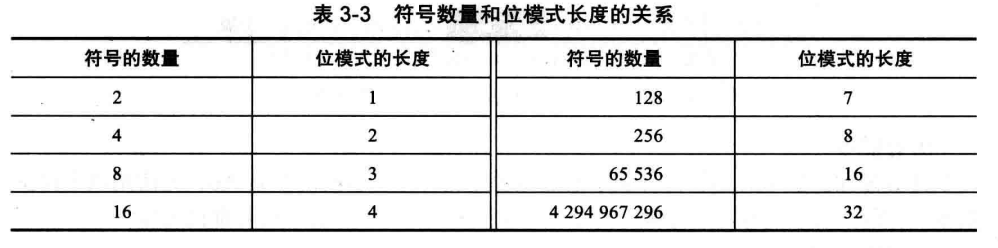
答: 这主要取决于该语言集中到底有多少不同的符号,即在一种语言中,表示某一符号的位模式的长度取决于该语言中所使用的符号的数量。更多的符号意味着更长的位模式。
例如,如果要创建的某个虚构的语言仅仅使用大写英文字母,则只需要26个符号,相应地这种语言的位模式至少需要表示26个符号,通常每个字母占用1字节。
例如,如果对于中文,可能需要更多的符号,通常每个文字占有2~4字节(与字符编码有关)。
位模式的长度与符号的数量关系是呈对数的(其表达式为:位模式长度 = log2 符号数量),如果需要2个符号,位模式长度将是1位(log2 2=1),如果需要4个符号,位模式长度将是2位(log2 4=2).
1位的位模式能表示2种不同的形式:0,1
2位的位模式能表示4种不同的形式:00, 01, 10和11
代码与编码区别
代码:不同的位模式集合被设计用于表示文本符号,其中每一个集合我们称之为代码。
编码:表示符号的转换过程被称为编码。
现代计算机中常用的编码如下所示:
ASCII : 美国信息交换标准码,由美国国家标准协会(ANSI) 开发,代码使用7位表示每个符号,即该代码可以定义2^7=128种不同的符号.Unicode :由硬件和软件制造商联合设计的编码,设计代码使用32位并能表示最大达2^32=4 294 967 296个符号,该代码不同部分被分配用于表示来自世界上不同语言的符号,以及表示图像和特殊符号。(PS: 如今ASCII是Unicode的一部分)其他编码 : 鉴于Unicode的优势,这些编码变得不太流行,此处简单了解即可。
字节与字符的区别
字节(Byte):是计量单位,表示数据量多少,是计算机信息技术用于计量存储容量的一种计量单位
字符(Character):计算机中使用的字母、数字、字和符号,比如’A’、’B’、’$’、’&’等字符。
现代计算机中不同编码占用的字节情况(考试中以及在开发中处理中文字符时会涉及):
3.4 音频存储 音频表示声音或音乐,它是随时间变化的实体,我们只能在每一时刻度量声音的密度。
音频本质上不同于数字与文本数据,音频是模拟数据的例子,即使我们能够在一段时间度量所有的值,也不能把它全部存在计算机内存中,因为可能需要无限数量的内存单元。
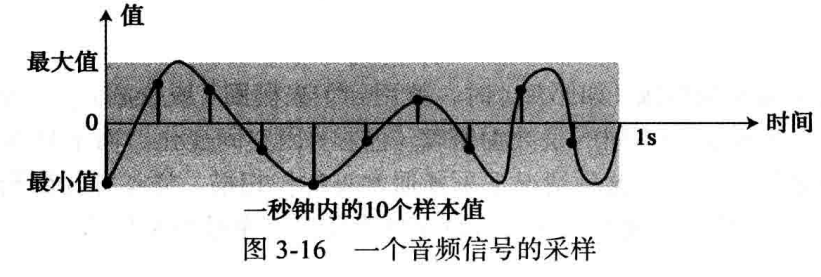
所以当我们讨论用计算机内存存储声音时,我们的意思是存储一个音频信号的密度,例如,每隔一段时间(一秒钟,一小时)来自麦克风的信号。
weiyigeek.top-音频信号采集
采样、量化、编码
计算机中要存储音频的需要进行采样、量化、编码等关键操作步骤:
采样 : 我们需要在模拟信号上选择数量有限的点来度量它们的值并记录下来,例如上图中音频信号我们选择10 个样本,我们可以记录这些值来表现模拟信号。
Q: 下一个逻辑问题是我们每秒钟需要多少样本才能还原出原始信号的副本?
如果信号是平坦的,则需要很少的样本;如果信号变化剧烈,则需要更多的样本,所以说样本数量依赖于模拟信号中变化的最大数量。
采样率:通常每秒40 000个样本的釆样率对音频信号来说是足够好的。
量化 : 指的是将样本的值截取为最接近的整数值的一种过程(可以理解为四舍五入),从每个样本测量来的值是真实的数字, 为每个样本使用一个无符号的数(位模式)会更简便,所以需要针对其进行量化。
例如,如果实际的值为17.2,就可截取为17; 如果值为17.7,就可截取为18。
编码 :量化的样本值需要被编码成位模式,某一些系统为样本赋正值或负值,另一些仅仅移动曲线到正的区间从而只赋正值,换言之,一些系统使用无符号整数来表示样本,而另一些使用有符号的整数来做。
毎样本位: 对于每个样本系统需要决定分配多少位 ,每样本位的数量有时称为位深度,尽管在过去仅有8位分配给声音样本,现在每样本16、24甚至32位都是正常的。
位率:如果我们称位深度或每样本位的数量为B,每秒样本数为S,我们需要为每秒的音频存储SxB位,该乘积有时称为位率R。
例如,如果我们使用每秒40 000个样本以及每样本16 位,位率是R=40 000 x 16=640 000 b/s=640 KB/s。
声音编码标准 AAC 、AC-3、AMR、WMA、ALAC、APE、FLAC、PCM、DSD、WAV、AIFF、MIDI等主流音频编码格式解析。
MP3 : 最通用最常见的格式, 它采用每秒44 100个样本以及每样本16 位, 结果信号达到705 600 b/s的位率,再用去掉那些人耳无法识别的信息的压缩方法进行压缩。 (有损压缩)
AAC : 高级音频编码(Advanced Audio Coding)的缩写,是新一代的音频有损压缩技术,在苹果设备上是最为常用的格式,其格式后缀名有aac,mp4,m4a三种。(有损压缩)
AC-3:数字音频压缩标准 (Digital Audio Compression Standard)音频编码格式,是传说中的杜比实验室的杰作,著名的有损数据压缩的多媒体储存格式, 可以包括多达6个独立的声道,其最知名的是5.1声道技术。(有损压缩)
AMR:自适应多速率(Adaptive Multi-Rate)压缩音频编码格式,是一个使语音编码最优化的专利,专用于有效地压缩语音频率, 主要用于移动设备的音频压缩,压缩比非常高,但是音质比较差,主要用于语音类的音频。(有损压缩)
WMA: (Windows Media Audio),它是微软公司推出的与MP3格式齐名的一种新的音频格式。由于WMA在压缩比和音质方面都超过了MP3,在较低的采样频率下也能产生较好的音质,其后缀名为.wma, 但这种格式通常只能使用 Windows 自带的 MediaPlayer 来播放,与纯音频的媒体串流格式.ASF 类似。(无损压缩)
ALAC: (Apple Lossless Audio Codec) 苹果的无损音频压缩编码格式,ALAC与MP3的主要分别在于编码过程中,MP3会取消小部分高频及低频部分的音频数据,而ALAC则会如实记录,不会删除音频中任何细节数据。(无损压缩)
APE:它是Monkey’s Audio 公司提供的一种无损压缩音频格式,它可以通过无损压缩技术使庞大的 WAV 文件压缩掉近一半而基本不怎么损失音质。并且这个格式是完全的免费和开源。(无损压缩)
FLAC:损音频压缩编码(Free Lossless Audio Codec。FLAC是一种著名的自由音频压缩编码,其特点是无损压缩,不同于其他有损压缩编码如MP3 及AAC,它不会破坏任何原有的音频资讯,其后缀格式为.flac。(无损压缩)
PCM: 脉冲编码调制(Pulse Code Modulated Audio),是目前计算机应用中最高保真水平的音频编码格式,PCM音频数据是未经压缩的音频采样数据裸流,它是由模拟信号经过采样、量化、编码转换成的标准的数字音频数据,通常CD唱片都采用此格式。(无压缩 )
DSD:直接比特流数字(Direct Stream Digital)相对于PCM的最大优势是,具有极小的量化噪声, 超高的信噪比,这是音乐发烧友才会玩的格式。(无压缩 )
WAV:是微软公司(Microsoft)开发的一种声音文件格式,它是最接近无损的音乐格式,所以文件大小相对也比较大,也是很多音频处理软件默认保存的音频格式。(无压缩 )
AIFF:音频交换文件格式(Audio Interchange File Format)的英文缩写,是Apple公司开发的一种声音文件格式,是为了对抗微软的WAV而开发。(无压缩 )
MIDI(Musical Instrument Digital Interface)格式被经常玩音乐的人使用,MIDI允许数字合成器和其他设备交换数据。最大作用在于用电脑音乐作曲。所以它并不是录制的声音而是制作出的声音,其后缀格式为.mid。(无压缩 )
3.5 图像存储 在计算机中存储图像使用两种不同的技术:光栅图或矢量图。
(1) 光栅图 当我们需要存储模拟图像(如照片)时,就用到了光栅图(或位图),一张照片由模拟数据组成,不同的是数据密度(色彩)因空间变化,而不是因时间变化,同样需要针对其样本数据进行采样(扫描)。
样本称为像素(代表图像元素),换言之,整个图像被分成小的像素,每个像素假定有单独的密度值。
1.解析度 : 在图像处理中的扫描率称为解析度,如果解析率足够高,人眼不会看出在重现图像中的不连续。
2.色彩深度 : 用于表现像素的位的数量,即色彩深度,依赖于像素的颜色是如何由不同的编码技术来处理的,我们的眼睛有不同类型的感光细胞,一些响应红、黄、蓝三原色(也叫RGB), 而另一些仅仅响应光的密度。
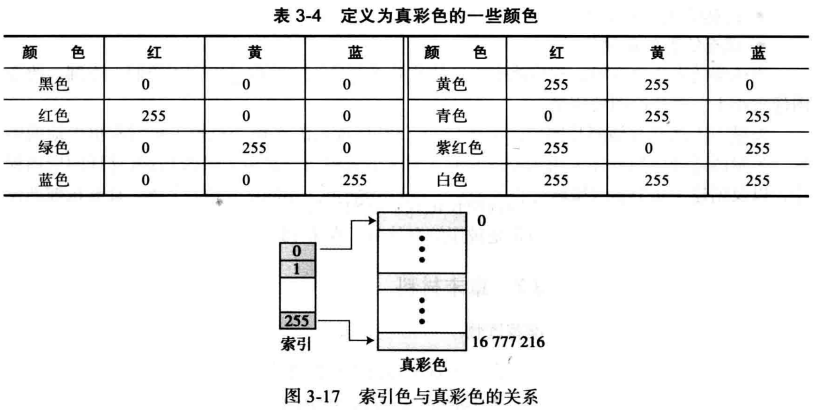
真彩色:用于像素编码的技术之一称为真彩色,它使用24位来编码一个像素(可以表达 16777216 种颜色),在该技术中每个三原色(RGB)都表示为8位,所以每种色彩都由0〜255之间的三维数字表示。
索引色:索引色(或调色板色)模式仅使用真彩色里其中的一部分,因为真彩色模式使用了超过1600万种的颜色,许多应用程序不需要如此大的颜色范围,在该模式中每个应用程序从大的色彩集中选择一些颜色(通常是256种)并对其建立索引,对选中的颜色赋一个0〜255之间的值,对索引的使用减少了需要存储一个像素所需要的位的数量。(PS: 类似艺术家可能在他们的画室用到很多种颜色,但一次仅用到他们调色板中的一些。)
例如,真彩模式需要24位来储存一个像素,索引色模式通常使用256个索引,这需要8位来存储同样的像素。
例如,一部高质量的数码相机要用几乎3百万像素拍摄一张3X5英寸的相片。
真彩色模式存储所需要的位的数量:3 000 000 x 24 = 72 000 000
索引色模式存储所需要的位的数量:3 000 000 x 8 = 24 000 000
3.图像编码标准
在计算机中常用的图像编码的标准是JPEG、PNG、GIF等
温馨提示:光栅图有两个缺点,即文件体积太大和重新调整图像大小有麻烦,放大光栅图像意味着扩大像素,所以放大后的图像看上去很粗糙。
扩展知识: 一个字节8比特,像素通常表示位图(bitmap)中的一个点。
对于 黑白图像(二值图像)一个详像素用一个bit表示,所以1字节表示8像素
对于 灰度图,一个像素为 256 种状态正好2的8次方,因此1字节表示1像素
对于 RGB 图,一个像素为 256 x 256 x 256 种状态正好2的24次方,因此3字节表示1像素
(2) 矢量图 矢量图图像编码方法并不存储每个像素的位模式,一个图像被分解成几何图形的组合。
矢量图是由定义如何绘制这些形状的一系列命令构成的,当要显示或打印图像时,将图像的尺寸作为输入传给系统,于此同时系统会重新设计图像的大小并用相同的公式画出图像,所以每次绘制图像时公式也将重新估算一次,因此矢量图也称为几何模型或面向对象图形。
矢量图适合应用程序采用主要的几何元素来创建图像。它用于诸如Flash 这样的应用程序,以及创建TrueType (微软、苹果公司)和PostScript (Adobe 公司)字体,计算机辅助设计(CAD) 也使用矢量图进行工程绘图。
例如,线段、矩形或圆形,每个几何形状由数学公式表达。
一个圆的半径r。
圆心的位置。
绘制的线型和颜色。
填充的类型和颜色。
温馨提示:当该圆的大小改变时,程序改变半径的值并重新计算这些信息以便再绘制一个圆,改变图像大小不会改变绘图的质量。
温馨提示:矢量图不适合存储照片图像的细微精妙,推荐使用JPEG 或GIF 光栅图提供了更好和更生动的图片。
3.6 视频存储 视频是图像(称为帧)在时间上的表示,一部电影就是一系列的帧一张接一张地播放而形成运动的图像。换言之,视频是随空间(单个图像)和时间(一系列图像)变化的信息表现。
所以在计算机中我们也就知道如何储存视频,它将每一幅图像或帧转化成一系列位模式并储存,将这些图像组合起来就可表示视频。
温馨提示:现在视频通常是被压缩存储的,常常使用的*MPEG*(Moving Picture Experts Group,动态图像专家组)技术针对常视频进行压缩。