[TOC]
计算机科学导论学习笔记 第 5 部分 数据组织与抽象 此部分包含第11 、12 、13 和14 章,讨论了数据结构、抽象数据类型、文件结构以及数据库原理。
在计算机科学中,原子数据汇集成记录、文件和数据库,而数据抽象使得程序员能创建关于数据的抽象观念。
原文地址: https://mp.weixin.qq.com/s/pdA3qGYV_k6HmPWC2j0NuA
12.抽象数据类型 抽象数据类型(abstact data type, ADT) 比上一章讨论的数据结构(数组、记录、链表)处于更高抽象层的数据类型,实际上ADT也是使用数据结构来实现的。
本章将讨论各种不同的抽象数据类型,例如:栈、队列、广义线性列表、树、二叉数、二叉搜索树和图。
抽象数据类型(ADT) :是数据类的定义和应用于数据的操作定义的集合。例如,求某个列表中数字之和,则需要选择数字类型(整数或实数)以及定义运算(加法)。
换言之,ADT的用户只需要知道对数据类型可用的一组操作,而不需要知道它们是如何应用的
12.1 定义模型 (1) 抽象数据类型定义 此处我们正式地定义抽象数据类型,抽象数据类型就是与对该数据类型有意义的操作封装在一起的数据类型, 然后用它封装数据和操作并对用户隐藏。
抽象数据类型:
1.数据的定义。
(2) 简单与复杂的ADT 简单抽象数据类型 ADT)作为语言的整数部分,
例如,C语言定义了称为整数的简单抽象数据类型(整型、浮点型、布尔型、字符、指针),还定义了在数据类型上应用的几种操作(加、减、乘、除等)。
例如,z = x + y ,即希望X的值(整数)被加到y的值(整数)上,其结果被命名为z整数,此时程序员并不需要知道加法是如何进行的。
在前一章我们学到计算机是如何执行加法运算的:把两个整数以补码的格式存储在内存地址中,把它们装入CPU的寄存器中,进行二进制相加,把结果回存到另一个内存地址中,此时对程序员来说是透明的。
C语言中的整数就是一个带有预定义操作的简单抽象数据类型,程序员不必关注操作是如何进行的。
复杂抽象数据类型
前面我们知道了许多编程语言都实现了几种简单的抽象数据类型,但许多有用的复杂抽象数据类型却没有实现,例如表抽象数据类型、栈抽象数据类型、队列抽象数据类型。为了效率,应该建立这些抽象数据类型,通常将它们存储在计算机库中,以便使用。
ADT包含了一组允许程序员使用的操作的定义,而这些操作的实现是隐藏的。此种不需详细说明实现过程的泛化操作称为抽象,我们抽取了过程的本质,而隐藏了实现的细节,而抽象概念意味着:
1.知道一个数据类型能做什么。
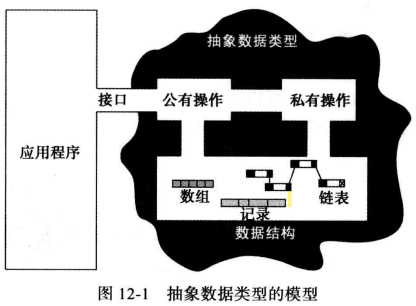
(3) 抽象数据类型的模型 下图中不规则轮廓中的浅阴影区域部分表示模型,在这个抽象区域内部是该模型的两个部分:基本数据结构和数据操作(公有的和私有的)。
应用程序只能通过接口访问公有操作,然后再通过其访问私有操作, 而数据结构(如数组、记录、链表)包含着在抽象数据类型里面,被公有和私有操作共同使用。
接口 :公有操作和传给或从这些操作返回的数据的列表
私有操作 :是抽象数据类型内部用户使用的,它依赖于抽象数据类型实现时所选择的数据结构。
weiyigeek.top-抽象数据类型的模型
(4) 抽象数据类型的实现 由于计算机编程语言不提供抽象数据类型包(类),需要程序员自行实现并存储在库中。
所以下一子节将主要,介绍实现一些常见的抽象数据类型(栈、队列、线性表、树、图)等。
12.2 栈 (Stack) (1) 栈的介绍 栈 是一种限制线性列表,该类列表的添加和删除操作只能在”栈顶”端实现,它是后进先出(LIFO)数据结构。
FIFO:全称First in, First out,先进先出。
LIFO:全称Last in, First out,后进先出。
即输入插入是顺序 5, 10, 15, 20,而输出顺序则是 20 ,15 ,10, 5。
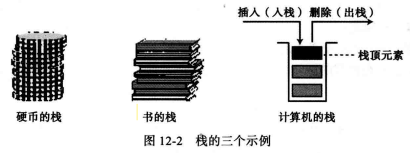
例如,人们在日常生活中使用不同类型的栈,如一堆硬币或一堆书。
weiyigeek.top-栈的示例图
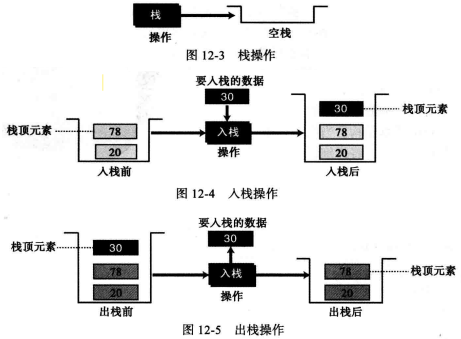
(2) 栈的操作 尽管栈有很多操作,但基本操作有4种∶建栈(stack)、入栈(push)、出栈(pop)和空(empty)。
1) 建栈(Stack) :该操作是创建一个空栈,格式如stack(stackName)。
2) 入栈(Push) :入栈操作在栈顶添加新的元素,格式如push(stackName, dataItem), stackName 是栈的名字,dataItem是要插在栈顶的数据。
3) 出栈(Pop) : 出栈操作将栈顶元素移走,格式如pop(stackNmae,dataItem),stackName 是栈的名字,dataltem是从栈中移走的数据。
4) 空(empty) :空操作检查栈的状态,格式如empty(stackName, stackName是栈的名字,如果栈为空返回True,否则返回False。
weiyigeek.top-栈的操作图
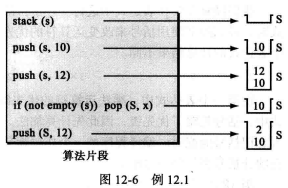
(3) 栈的抽象数据类型 定义: 只能在栈顶存取的数据项表。
操作: 创建空栈,栈顶插入元素,栈顶插入元素,移除栈顶元素,检查栈的状态。
weiyigeek.top-栈操作算法片段图
(4) 栈的应用 应用可分为4大类:倒转数据、配对数据、数据延迟使用和回溯步骤。
1) 倒转数据 : 需要一组给定的数据项重新排序,使得首尾元素互换,中间的所有元素也相应地进行交换。
例如:表(2, 4, 7, 1, 6, 8)变成表(8, 6, 1, 7, 4, 2), 即将得到倒排顺序的数字。
任何计算机语言中的打印指令都是从左到右打印字符的,但算法是从右到左建立数字的,此时我们使用栈的倒转特性(LIFO结构)来解决这个问题。
2) 配对数据项 : 需要在表达式中进行一些字符的配对。
例如,当用计算机语言写一个数学表达式时,我们经常使用括号来改变运算符的优先级 3X(6+2) = 24
当输入一个带有许多括号的表达式时, 通常编译程序(编译器)使用栈来检査所 有的开括号都与闭括号配对。
weiyigeek.top-配对数据项伪代码图
(5) 栈的实现 栈主要包含两个操作,入栈和出栈,也就是在栈顶插入一个数据和从栈顶删除一个数据。
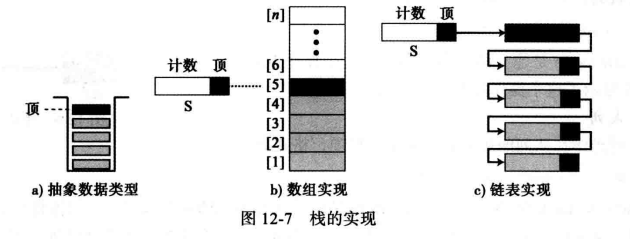
栈抽象数据类型可以使用数组也可以使用链表来实现,下图显示了栈抽象数据类型的例子,以及我们是如何实现栈的。
weiyigeek.top-栈的实现
数组实现( 顺序栈):** 创建有两个域的记录,第一个域用来存储关于数组的信息:我们把它当作计数域,在任何时刻其中显示的是栈中数据项的数目,第二个域是含有顶元素序号的一个整数。
链表实现( 链式栈):** 节点有两个域,一个计数器和一个指向栈顶元素的指针。
此处使用Go语言实现链式栈:
[TOC]
计算机科学导论学习笔记 第 5 部分 数据组织与抽象 此部分包含第11 、12 、13 和14 章,讨论了数据结构、抽象数据类型、文件结构以及数据库原理。
在计算机科学中,原子数据汇集成记录、文件和数据库,而数据抽象使得程序员能创建关于数据的抽象观念。
原文地址: https://mp.weixin.qq.com/s/pdA3qGYV_k6HmPWC2j0NuA
12.抽象数据类型 抽象数据类型(abstact data type, ADT) 比上一章讨论的数据结构(数组、记录、链表)处于更高抽象层的数据类型,实际上ADT也是使用数据结构来实现的。
本章将讨论各种不同的抽象数据类型,例如:栈、队列、广义线性列表、树、二叉数、二叉搜索树和图。
抽象数据类型(ADT) :是数据类的定义和应用于数据的操作定义的集合。例如,求某个列表中数字之和,则需要选择数字类型(整数或实数)以及定义运算(加法)。
换言之,ADT的用户只需要知道对数据类型可用的一组操作,而不需要知道它们是如何应用的
12.1 定义模型 (1) 抽象数据类型定义 此处我们正式地定义抽象数据类型,抽象数据类型就是与对该数据类型有意义的操作封装在一起的数据类型, 然后用它封装数据和操作并对用户隐藏。
抽象数据类型:
1.数据的定义。
(2) 简单与复杂的ADT 简单抽象数据类型 ADT)作为语言的整数部分,
例如,C语言定义了称为整数的简单抽象数据类型(整型、浮点型、布尔型、字符、指针),还定义了在数据类型上应用的几种操作(加、减、乘、除等)。
例如,z = x + y ,即希望X的值(整数)被加到y的值(整数)上,其结果被命名为z整数,此时程序员并不需要知道加法是如何进行的。
在前一章我们学到计算机是如何执行加法运算的:把两个整数以补码的格式存储在内存地址中,把它们装入CPU的寄存器中,进行二进制相加,把结果回存到另一个内存地址中,此时对程序员来说是透明的。
C语言中的整数就是一个带有预定义操作的简单抽象数据类型,程序员不必关注操作是如何进行的。
复杂抽象数据类型
前面我们知道了许多编程语言都实现了几种简单的抽象数据类型,但许多有用的复杂抽象数据类型却没有实现,例如表抽象数据类型、栈抽象数据类型、队列抽象数据类型。为了效率,应该建立这些抽象数据类型,通常将它们存储在计算机库中,以便使用。
ADT包含了一组允许程序员使用的操作的定义,而这些操作的实现是隐藏的。此种不需详细说明实现过程的泛化操作称为抽象,我们抽取了过程的本质,而隐藏了实现的细节,而抽象概念意味着:
1.知道一个数据类型能做什么。
(3) 抽象数据类型的模型 下图中不规则轮廓中的浅阴影区域部分表示模型,在这个抽象区域内部是该模型的两个部分:基本数据结构和数据操作(公有的和私有的)。
应用程序只能通过接口访问公有操作,然后再通过其访问私有操作, 而数据结构(如数组、记录、链表)包含着在抽象数据类型里面,被公有和私有操作共同使用。
接口 :公有操作和传给或从这些操作返回的数据的列表
私有操作 :是抽象数据类型内部用户使用的,它依赖于抽象数据类型实现时所选择的数据结构。
weiyigeek.top-抽象数据类型的模型
(4) 抽象数据类型的实现 由于计算机编程语言不提供抽象数据类型包(类),需要程序员自行实现并存储在库中。
所以下一子节将主要,介绍实现一些常见的抽象数据类型(栈、队列、线性表、树、图)等。
12.2 栈 (Stack) (1) 栈的介绍 栈 是一种限制线性列表,该类列表的添加和删除操作只能在”栈顶”端实现,它是后进先出(LIFO)数据结构。
FIFO:全称First in, First out,先进先出。
LIFO:全称Last in, First out,后进先出。
即输入插入是顺序 5, 10, 15, 20,而输出顺序则是 20 ,15 ,10, 5。
例如,人们在日常生活中使用不同类型的栈,如一堆硬币或一堆书。
weiyigeek.top-栈的示例图
(2) 栈的操作 尽管栈有很多操作,但基本操作有4种∶建栈(stack)、入栈(push)、出栈(pop)和空(empty)。
1) 建栈(Stack) :该操作是创建一个空栈,格式如stack(stackName)。
2) 入栈(Push) :入栈操作在栈顶添加新的元素,格式如push(stackName, dataItem), stackName 是栈的名字,dataItem是要插在栈顶的数据。
3) 出栈(Pop) : 出栈操作将栈顶元素移走,格式如pop(stackNmae,dataItem),stackName 是栈的名字,dataltem是从栈中移走的数据。
4) 空(empty) :空操作检查栈的状态,格式如empty(stackName, stackName是栈的名字,如果栈为空返回True,否则返回False。
weiyigeek.top-栈的操作图
(3) 栈的抽象数据类型 定义: 只能在栈顶存取的数据项表。
操作: 创建空栈,栈顶插入元素,栈顶插入元素,移除栈顶元素,检查栈的状态。
weiyigeek.top-栈操作算法片段图
(4) 栈的应用 应用可分为4大类:倒转数据、配对数据、数据延迟使用和回溯步骤。
1) 倒转数据 : 需要一组给定的数据项重新排序,使得首尾元素互换,中间的所有元素也相应地进行交换。
例如:表(2, 4, 7, 1, 6, 8)变成表(8, 6, 1, 7, 4, 2), 即将得到倒排顺序的数字。
任何计算机语言中的打印指令都是从左到右打印字符的,但算法是从右到左建立数字的,此时我们使用栈的倒转特性(LIFO结构)来解决这个问题。
2) 配对数据项 : 需要在表达式中进行一些字符的配对。
例如,当用计算机语言写一个数学表达式时,我们经常使用括号来改变运算符的优先级 3X(6+2) = 24
当输入一个带有许多括号的表达式时, 通常编译程序(编译器)使用栈来检査所 有的开括号都与闭括号配对。
weiyigeek.top-配对数据项伪代码图
(5) 栈的实现 栈主要包含两个操作,入栈和出栈,也就是在栈顶插入一个数据和从栈顶删除一个数据。
栈抽象数据类型可以使用数组也可以使用链表来实现,下图显示了栈抽象数据类型的例子,以及我们是如何实现栈的。
weiyigeek.top-栈的实现
数组实现( 顺序栈):** 创建有两个域的记录,第一个域用来存储关于数组的信息:我们把它当作计数域,在任何时刻其中显示的是栈中数据项的数目,第二个域是含有顶元素序号的一个整数。
链表实现( 链式栈):** 节点有两个域,一个计数器和一个指向栈顶元素的指针。
此处使用Go语言实现链式栈:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 package mainimport "fmt" type Node struct { data interface {} next *Node } type Stack struct { topeNode *Node } func NewStack () *Stack return &Stack{ nil , } } func (this *Stack) Push (value interface {}) this.topeNode = &Node{data:value, next:this.topeNode} } func (this *Stack) isEmpty () bool if this.topeNode == nil { return true } return false } func (this *Stack) Pop () interface if this.isEmpty(){ return nil } value := this.topeNode.data this.topeNode = this.topeNode.next return value } func (this *Stack) Top () interface if this.isEmpty(){ return nil } return this.topeNode.data } func (this *Stack) Print () if this.isEmpty(){ fmt.Println("empty Stack" ) } cur := this.topeNode for nil != cur{ fmt.Println(cur.data) cur = cur.next } } func main () fmt.Println("# Go Implementation Chain Stack......" ) demoStack := NewStack() demoStack.Push("Go" ) demoStack.Push("C" ) demoStack.Push("Java" ) fmt.Println("# Stack traversal ->" ) demoStack.Print() fmt.Println("# Pop Data ->" , demoStack.Pop()) fmt.Println("# TopeNode Data ->" , demoStack.Top()) fmt.Println("# Stack Empty ->" , demoStack.isEmpty()) }
执行结果:
补充,此时也贴上使用数组方式实现栈此种数据结构。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 package mainimport ( "errors" "fmt" ) type StackArray interface { Clear() Size()int Pop() interface {} Push(data interface {}) isEmpty() bool isFull() bool } type ArrayList struct { dataStore [] interface {} theSize int } type Stack struct { myarray *ArrayList capsize int } func New () *ArrayList list:=new (ArrayList) list.dataStore=make ([]interface {},0 ,10 ) list.theSize=0 fmt.Println("new >>>" ,list.theSize,cap (list.dataStore)) return list } func NewStack (count int ) *Stack mystack:=new (Stack) mystack.myarray=New() mystack.capsize=count return mystack } func (list *ArrayList) Append (newval interface {}) list.dataStore=append (list.dataStore,newval) fmt.Println("index = " ,list.theSize,",data = " ,newval,cap (list.dataStore)) list.theSize++ } func (list *ArrayList ) Remove (index int ) error if index <0 || index >=list.theSize{ return errors.New("索引越界" ) } list.dataStore=append (list.dataStore[:index],list.dataStore[index+1 :]...) list.theSize-- return nil } func (list *ArrayList ) Clear () list.dataStore=make ([]interface {},0 ,10 ) list.theSize=0 } func (mystack *Stack) Clear () mystack.myarray.Clear() mystack.myarray.theSize=0 } func (mystack *Stack) Size () int return mystack.myarray.theSize } func (mystack *Stack) isEmpty () bool if mystack.myarray.theSize==0 { return true }else { return false } } func (mystack *Stack) isFull () bool if mystack.capsize <= mystack.myarray.theSize{ return true }else { return false } } func (mystack *Stack) Pop () interface if !mystack.isEmpty(){ last:=mystack.myarray.dataStore[mystack.myarray.theSize-1 ] mystack.myarray.Remove(mystack.myarray.theSize-1 ) return last; } return nil } func (mystack *Stack) Push (data interface {}) if !mystack.isFull(){ mystack.myarray.Append(data) } } func main () mystack :=NewStack(12 ) mystack.Push(1 ) mystack.Push(2 ) mystack.Push(3 ) mystack.Push(4 ) mystack.Push(5 ) mystack.Push(6 ) mystack.Push(7 ) mystack.Push(8 ) mystack.Push(9 ) mystack.Push(10 ) mystack.Push(11 ) mystack.Push(12 ) fmt.Println("弹栈 >>> " ) fmt.Println(mystack.Pop()) fmt.Println(mystack.Pop()) fmt.Println(mystack.Pop()) fmt.Println(mystack.Pop()) }
执行结果:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 new >>> 0 10 压栈 >>> index = 0 ,data = 1 10 index = 1 ,data = 2 10 index = 2 ,data = 3 10 index = 3 ,data = 4 10 index = 4 ,data = 5 10 index = 5 ,data = 6 10 index = 6 ,data = 7 10 index = 7 ,data = 8 10 index = 8 ,data = 9 10 index = 9 ,data = 10 10 index = 10 ,data = 11 20 index = 11 ,data = 12 20 弹栈 >>> 12 11 10 9
本节总结: 栈是一种”操作受限”的线性表,只允许在一端插入和删除数据, 当某个数据集合只涉及在一端插入和删除数据,并且满足后进先出(LIFO)、先进后出的(FILO)特性,我们就应该首选“栈”这种数据结构。
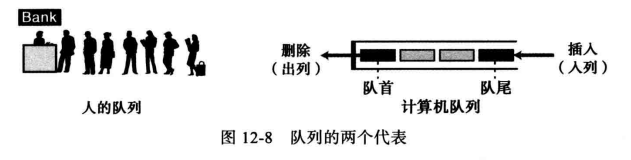
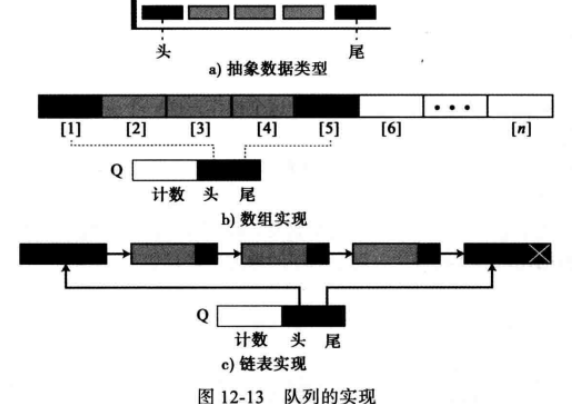
12.3 队列 (Queue) (1) 队列的介绍 队列也是一种线性列表,该表中的数据只能在称为尾部的一端插入,并且只能在称之为头部的一端删除。限制确保了数据在队列中只能按照它们存入的顺序被处理。换言之,队列就是先进先出(FIFO)结构。
队列其实在日常生活中很常见的,例如公交车站排队上车,公园入口处排队检票,等待电话接线员回复的一系列电话也是一个队列,等待计算机处理的一系列等待任务也是队列。
weiyigeek.top-队列介绍
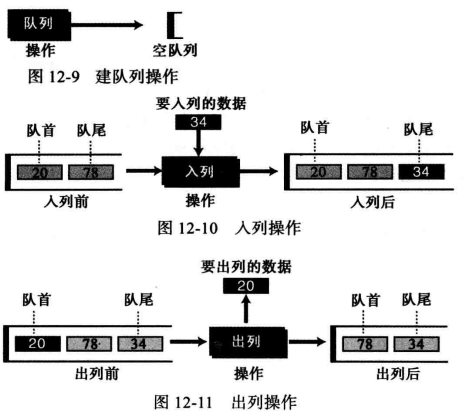
(2) 队列的操作 尽管我们可以为队列定义许多操作,但有4个是基本的:建队列、入列、出列和空,定义如下。
1 2 3 4 5 6 7 8 > newQueue(queueName): 建队列建立一个空队列. > enqueue(queueName, dataItem): 入列操作在队列的尾部插入一个数据项. > dequeue(queueName, dataltem): 出列操作删除队列前端的数据项. > isEmpty(queueName): 空操作检査队列的状态,若队列为空返回为真,否则为假.
weiyigeek.top-队列操作
(3) 队列抽象数据类型 定义:通过前面学习,我们知道队列是一种线性列表,该表中的数据只能在称为头部的一端删除,并且只能在称为尾部的一端插入。
newqueue: 创建一个空的队列。
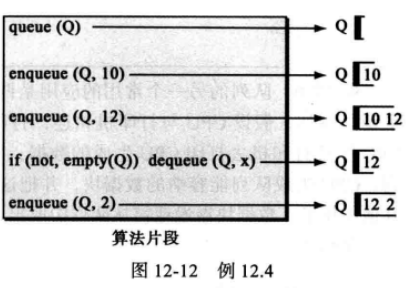
下图显示了应用原先定义在队列Q上的操作的算法片段, 在第4个操作在队首出列前检査队列的状态,队首元素的值被存储在变量x中,它会在算法片段结束时,它将被自动丢弃。
weiyigeek.top-队列抽象数据类型
(4) 队列的应用 队列除了在生活着常常看到,它也是最常用的数据处理结构之一,在所有的操作系统以及网络中都有队列的身影,在其他技术领域更是数不胜数。
例如,在计算机系统中常见就是使用队列来完成对作业或对系统设备(如打印池) 的处理,而队列应用不单单如此,在线电子商务应用程序中实现web或PC端在线交流、任务和指令流程(程序之间),在网络中实现数据有序传输。
(5) 队列的实现 队列抽象数据类型可以使用数组或链表来实现,下图中显示了一个有5个数据项的队列抽象数据类型的例子以及我们是如何实现队列的。
weiyigeek.top-队列的实现
此处我们使用Go语言进行队列链的实现,示例代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 package mainimport "fmt" type Node struct { data interface {} next *Node } type Queue struct { headNode *Node lastNode *Node } func NewQueue () *Queue return &Queue{ nil , nil , } } func (this *Queue) isEmpty () bool if this.headNode == nil { return true } return false } func (this *Queue) enqueue (value interface {}) if this.headNode == nil { this.lastNode = &Node{data:value, next:nil } this.headNode = this.lastNode } else { this.lastNode.next = &Node{data:value, next:nil } this.lastNode = this.lastNode.next } } func (this *Queue) dequeue () interface if this.isEmpty(){ return nil } value := this.headNode.data this.headNode = this.headNode.next return value } func (this *Queue) Head () interface if this.isEmpty(){ return nil } return this.headNode.data } func (this *Queue) Last () interface if this.isEmpty(){ return nil } return this.lastNode.data } func (this *Queue) Print () if this.isEmpty(){ fmt.Println("empty Queue" ) } cur := this.headNode for nil != cur{ fmt.Println(cur.data) cur = cur.next } } func main () fmt.Println("Go Implementation Chain Queue ......" ) demoQueue := NewQueue() demoQueue.enqueue("1.Go" ) demoQueue.enqueue("2.C" ) demoQueue.enqueue("3.Java" ) demoQueue.enqueue("4.Python" ) fmt.Println("# Queue 队列头部数据: " , demoQueue.Head()) fmt.Println("# Queue 队列尾部数据: " , demoQueue.Last()) fmt.Println("# 遍历队列数据: " ) demoQueue.Print() fmt.Println("# 弹出队列中头部数据并指向下一数据: " , demoQueue.dequeue()) fmt.Println("# 弹出后此时 Queue 队列头部数据: " , demoQueue.Head()) }
执行结果:
1 2 3 4 5 6 7 8 9 10 Go Implementation Chain Queue ...... 1.Go 2.C 3.Java 4.Python
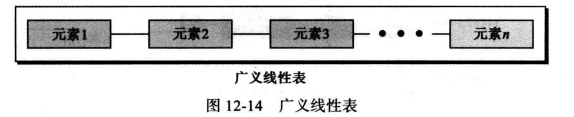
12.4 广义线性表(List) (1) 广义线性表的介绍 前两节中介绍的栈和队列都是限制线性表,而此小节讲解的广义线性表是像插入和删除等操作可以在其中任何地方进行的表,即我们可以在表头、表中间或表尾进行插入或删除。
广义线性表定义具有如下特性:
元素具有相同的类型 ;
元素顺序排列,这意味着有第一个元素和最后一个元素;
除第一个元素外每个元素都有唯一的前驱(上一个元素) ;除最后一个元素外每个元素都有唯一的后继(下一个元素) ;
每个元素是一个带有关键字段 的记录;
元素按关键字值排序。
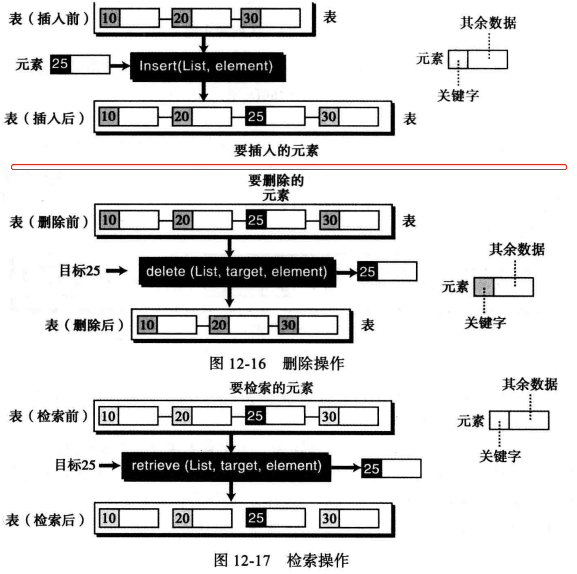
(2) 广义线性表的操作 此处讨论广义线性表的常用操作,即建表、插入、删除、检索,遍历和空,定义如下。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 newList(listname) insert(listname,element) delete(listname,target,element) retrieve(listname,target,element) traverse(listName,action) isEmpty(listName)
广义线性表部分操作图示:
weiyigeek.top-广义线性表
(3) 广义线性表抽象数据类型 类型定义:一个有序的数据项表 ,所有的项具有相同类型。
操作总结:
newList: 创建一个空表
insert:在表中插入一个元素。
delete: 从表中删除一个元素。
retrieve: 从表中检索一个元素
traverse : 顺序地遍历表。
isEmpty:检查表的状态。
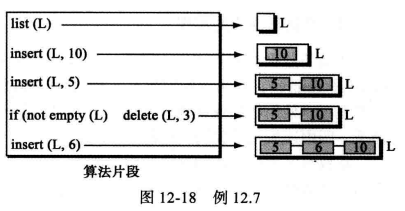
下图显示了在表L上应用前面定义的操作的一个算法片段。特别注意,通常在删除表中的数据项时,需要调用空操作方法判断表是否为非空。
weiyigeek.top-广义线性表抽象数据类型
(4) 广义线性表的应用 其通常应用于元素被随机存取或顺序存取的情况。
例如,在大学里,线性表可以用来存储每个学期入学的学生信息,我们可以使用线性表进行学生信息的增、删、改、查等操作,或者假设辅导教师在学期末要打印所有学生的记录。
(5) 广义线性表的实现 广义线性表抽象数据类型可以使用数组或链表来实现,通过前面的学习可知在线性表抽象数据类型层次上,利用6个操作对表中的元素进行处理。
在数组实现中,我们有带有两个域的记录。第一个域用来存储关于数组的信息:我们把它当作计数域,其中显示的是表中当前数据项的数目,第二个域是含有表中首元素序号的一个整数。
链表的实现是相似的:我们有一个有表名字的额外节点,这个节点也有两个域:一个计数器和一个指向首元素的指针。
此处,以Go语言为例分别演示数组与链表进行广义线性表的实现。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 package mainimport ( "errors" "fmt" ) const MaxSize int = 10 type SeqListClass struct { data []int length int } func NewList () *SeqListClass if MaxSize == 0 { return nil } return &SeqListClass{ data: make ([]int , MaxSize, MaxSize), length: 0 , } } func (this *SeqListClass) creatList (data []int , n int ) (err error) for i := 0 ; i < n; i++ { this.data[i] = data[i] } this.length = n fmt.Println(this.data) return nil } func (this *SeqListClass) dispList () (err error) if this.length == 0 { fmt.Println("顺序表为0!" ) } for i := 0 ; i < this.length; i++ { fmt.Printf("%d\t" , this.data[i]) } return nil } func (this *SeqListClass) listLength () int return this.length } func (this *SeqListClass) getEleme (i int ) (int , error) if i < 0 || i > this.length { return -1 , errors.New("out of range!" ) } return this.data[i-1 ], nil } func (this *SeqListClass) LocateElem (value int ) (int , error) var i int for i = 0 ; i < this.length; i++ { if value == this.data[i] { break } } if i >= this.length { return -1 , errors.New("out of range" ) } return i + 1 , nil } func (this *SeqListClass) ListInsert (i, value int ) error if i < 0 || i >= this.length { return errors.New("out of range" ) } for j := this.length; j >= i; j-- { this.data[j] = this.data[j-1 ] } this.data[i] = value this.length++ return nil } func (this *SeqListClass) ListDelete (i int ) error if i < 0 || i >= this.length { return errors.New("out of range" ) } for j := i; j < this.length; j++ { this.data[j] = this.data[j+1 ] } this.length-- return nil } func (this *SeqListClass) Reserve () for i := 0 ; i < this.length/2 ; i++ { tmp := this.data[i] this.data[i] = this.data[this.length-i-1 ] this.data[this.length-i-1 ] = tmp } } func main () lst := NewList() data := []int {12 , 2 , 13 , 4 , 23 , 10 , 5 , 8 } lst.creatList(data, 8 ) lst.dispList() n := lst.listLength() fmt.Println("表长为" , n) n, _ = lst.getEleme(5 ) fmt.Println("查找到元素为" , n) n, _ = lst.LocateElem(5 ) fmt.Println("查找到的位置为" , n) fmt.Println("插入前表长为" , lst.listLength() ) lst.ListInsert(4 , 5 ) fmt.Println("插入新元素后的列表为:" , lst.data) fmt.Println("插入后表长为" , lst.listLength() ) lst.ListDelete(5 ) fmt.Println("删除元素后的列表为:" , lst.data) fmt.Println("删除后表长为" , lst.listLength() ) lst.Reserve() fmt.Println("列表反转后为:" , lst.data) }
执行结果:
1 2 3 4 5 6 7 8 9 10 [12 2 13 4 23 10 5 8 0 0 ] 12 2 13 4 23 10 5 8 表长为 8 查找到元素为 23 查找到的位置为 7 插入前表长为 8 插入新元素后的列表为: [12 2 13 4 5 23 10 5 8 0 ] 插入后表长为 9 删除元素后的列表为: [12 2 13 4 5 10 5 8 0 0 ] 删除后表长为 8 列表反转后为: [8 5 10 5 4 13 2 12 0 0 ]
循环单链表和单链表大致一样,但不同的地方在于,尾指针并不是指向nil,而是指向表头https://studygolang.com/articles/14527 )
此处,使用Go语言演示循环单链表。1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 package mainimport ( "fmt" ) type object interface {}type node struct { data object next *node } type cLinkList struct { num uint64 head *node } func newList () *cLinkList return &cLinkList{ num: 0 , head: nil , } } func (this *cLinkList) getHead () *node return this.head } func (this *cLinkList) getNum () uint64 return (*this).num } func (this *cLinkList) appenData (data object) newNode := &node{data: data} if this.getNum() == 0 { (*this).head = newNode } else { cur := this.getHead() for ; (*cur).next != this.getHead(); cur = (*cur).next { } (*cur).next = newNode } (*newNode).next = (*this).getHead() (*this).num++ } func (this *cLinkList) insertData (index int , data object) newNode := &node{data: data} if index < 0 || uint64 (index) > this.getNum() { this.appenData(data) } else { cur := this.getHead() count := 0 for count < index-1 { cur = cur.next count++ } newNode.next = cur.next cur.next = newNode (*this).num++ } } func (this *cLinkList) removeData (data object) elem := &node{data: data} if elem == nil { fmt.Println("输入元素有误!" ) } cur := this.getHead() pre := &node{data: nil ,next: nil } prenode := &node{data: nil ,next: nil } for pre = cur; (*cur).data != (*elem).data; cur = (*cur).next { prenode = pre pre = (*pre).next } (*prenode).next = (*cur).next (*this).num-- } func (this *node) getTail () object return this.next } func (this *cLinkList) showList () if this.getNum() == 0 { fmt.Println("当前为空表!" ) } else { cur := this.head fmt.Print("当前元素为:" , cur.data) for cur.next != this.getHead() { if cur.next == this.getHead() { break } cur = cur.next fmt.Print("\t" ,cur.data) } } fmt.Println() } func main () lst := newList() for i := 0 ; i < 9 ; i++ { lst.appenData(i) } lst.showList() fmt.Println("节点数量" ,lst.getNum()) lst.insertData(6 , 64 ) lst.insertData(7 , 128 ) lst.showList() fmt.Println("当前节点数量" ,lst.getNum()) lst.removeData(6 ) lst.removeData(128 ) lst.showList() fmt.Println("当前节点数量" ,lst.getNum()) }
执行结果:1 2 3 4 5 6 7 当前元素为:0 1 2 3 4 5 6 7 8 节点数量 9 当前元素为:0 1 2 3 4 5 64 128 6 7 8 当前节点数量 11 当前元素为:0 1 2 3 4 5 64 7 8 当前节点数量 9
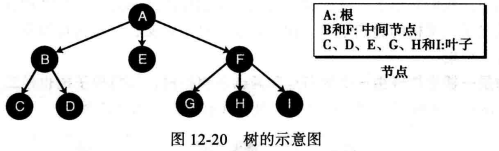
12.5 树 (1) 树的介绍 树在计算机科学中有许多应用,例如在目录文件索引处理中,最常用的抽象数据类型。树包括一组有限的元素,称为节点 (或顶点),同时包括一组有限的有向线段,用来连接节点,称为弧 。
如果树是非空的,其中有一个节点没有进入的弧,该节点称为根。树中的其他节点都可以沿着从根开始的唯一路径到达,该路径是指一系列相邻连接的节点序列。
树的结构通常被画成上下颠倒,根在顶部,我们可以把树中的顶点分成三类:根、叶子和内部节点 。
weiyigeek.top-树的介绍
在树中每种节点允许的外出弧和进入孤的数目,例如,
根的进入弧为0,其外出弧为0或者更多。
叶子的进入弧为1,其外出弧为0。
内部节点的进入弧为1,其外出弧为1或者更多。
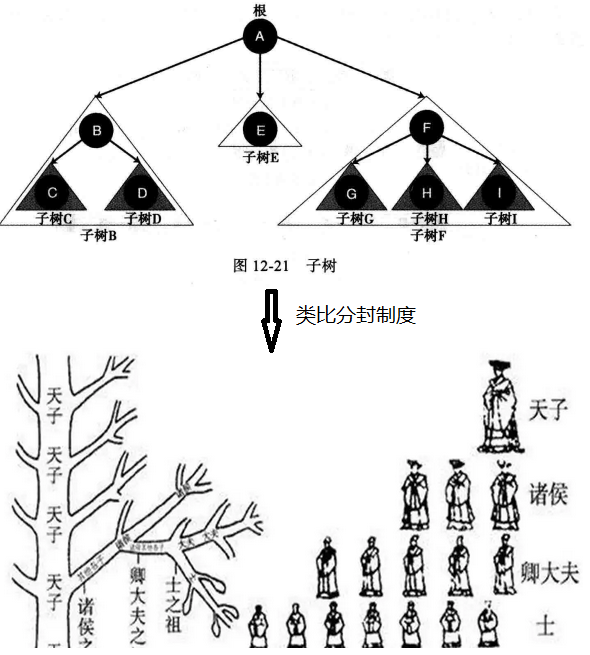
下图中显示了的树的所有子树,其类似于历史书中分封制度。
子节点:从一给定节点可以直接到达(通过一个弧)的节点称为子节点,
双亲:从其出发子节点可以直接到达的节点称为双亲。
兄弟节点:具有相同双亲的节点称为兄弟节点,
父节点(祖先):节点的子孙是指从该节点出发可以到达的所有节点,而从其出发所有的子孙都可以到达的节点称为祖先。
weiyigeek.top-树的类型
温馨提示:树中每个节点都有可能有子树。
(2) 二叉树的介绍 由于树的应用非常广泛,此处我们介绍一种最基本的抽象数据类型二叉树。
介绍:二叉树是一棵树,且其中没有一个节点所含有的子树的个数超过两个。换句话说,任一个节点只能有0、1或是2棵子树 ,这些子树被描述为左子树和右子树 。
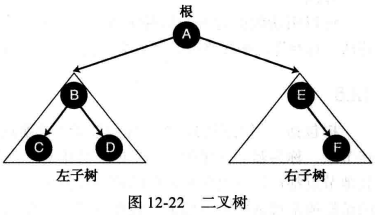
下图给出了一棵有两棵子树的二叉树,注意每一棵子树本身也是一棵二叉树 。
weiyigeek.top-二叉树
二叉树的递归定义:二叉树是一棵空树或由一个根节点和两棵子树构成,而每棵子树也是二叉树。
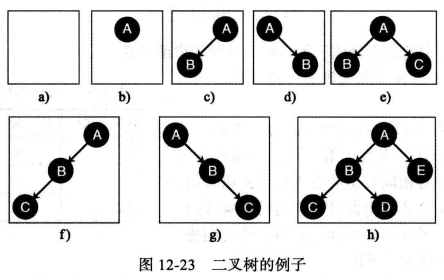
下图显示了8棵树,第一棵是空二叉树(有时称为零二叉树)。
weiyigeek.top-二叉树示例
(3) 二叉树的操作 二叉树中有6种最常用的操作是建树(创建一棵空树)、插入、删除、检索、空和遍历。本节只讨论二叉树的遍历,前5种超出了学习范围,有兴趣的朋友可以了解一哈。
1) 二叉树的遍历
二叉树遍历要求按照预定的顺序处理每一个节点且仅处理一次。
他有两种常用的遍历次序是深度优先 和广度优先 。
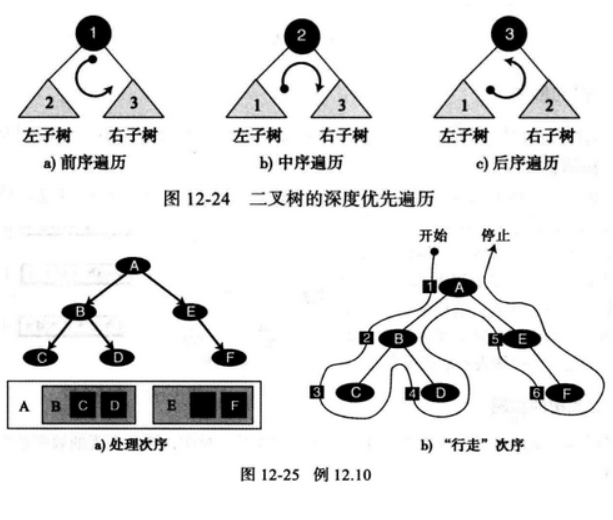
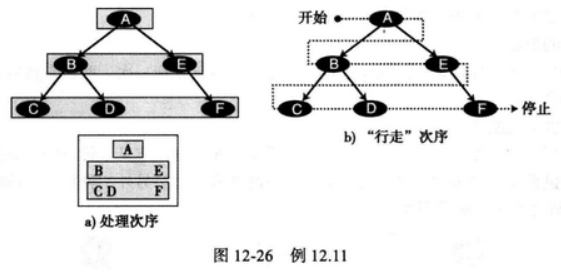
下图,显示了我们使用前序遍历访问树中的每个节点。
weiyigeek.top-二叉树的遍历
weiyigeek.top-二叉树的遍历示例
(4) 二叉树的应用 实际上二叉树在计算机科学中有许多应用,此处只简单介绍其中两种,即赫夫曼编码和表达式树。
1) 赫夫曼编码
赫夫曼编码是一种压缩技术,它使用二叉树来生成一个符号串的可变长度的二进制编码,在后续学习中我们会遇到。
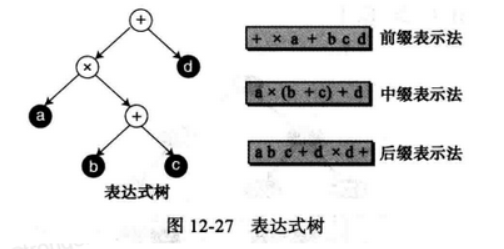
2) 表达式树
在表达式树中,根和内部节点是操作符,而叶子是操作数。此时三种标准的遍历(前序、中序和后序)分部表示了三种不同的表达式格式中缀、后缀、前缀。
在前缀表示中,操作符是处于两个操作数之前的; 前序遍历产生了前缀表达式。
在中缀表示中,操作符是处于两个操作数中间的;中序遍历产生了中缀表达式。
在后缀表示中,操作符是处于两个操作数之后的;后序遍历产生了后缀表达式。
即 前缀:+ A B 中缀:A + B 后缀:A B +
虽然我们在编程语言中使用中缀表示,但编译程序经常在计算表达式之前需要把它们转变为后缀表示,进行这个转换的一种方法就是建立表达式树。
weiyigeek.top-二叉树的表达式树
温馨提示: 注意只有中缀表示法需要括号。
(5) 二叉树的实现 二叉树可以使用数组或链表来实现,而实践中对于删除和插入操作,链表实现的效率要更高,所以更为流行。
此处,以Go语言为例用递归的方式遍历进行二叉树前序、中序、后续遍历演示。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 package mainimport "fmt" type Student struct { Name string Age int Score float32 left *Student right *Student } func preTree (tmp *Student) if tmp == nil { return } fmt.Println(*tmp) preTree(tmp.left) preTree(tmp.right) } func inTree (tmp *Student) if tmp == nil { return } inTree(tmp.left) fmt.Println(*tmp) inTree(tmp.right) } func postTree (tmp *Student) if tmp == nil { return } postTree(tmp.left) postTree(tmp.right) fmt.Println(*tmp) } func main () var root Student root.Name = "root" root.Age = 18 root.Score = 80 var left1 Student left1.Name = "left1" left1.Age = 19 left1.Score = 81 root.left = &left1 var right1 Student right1.Name = "right1" right1.Age = 20 right1.Score = 80 root.right = &right1 var left2 Student left2.Name = "left2" left2.Age = 29 left2.Score = 91 left1.left = &left2 fmt.Println("前序遍历函数(根左右)" ) preTree(&root) fmt.Println("中序遍历函数(左根右)" ) inTree(&root) fmt.Println("后序变量函数(左右根)" ) postTree(&root) }
执行结果:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 {root 18 80 0xc00005e150 0xc00005e180} {left1 19 81 0xc00005e1b0 } {left2 29 91 } {right1 20 80 } {left2 29 91 } {left1 19 81 0xc00005e1b0 } {root 18 80 0xc00005e150 0xc00005e180} {right1 20 80 } {left2 29 91 } {left1 19 81 0xc00005e1b0 } {right1 20 80 } {root 18 80 0xc00005e150 0xc00005e180}
示例2:非递归前序(深度优先遍历)思路:
1.声明一个栈
2.从栈中弹出一个节点cur
3.打印(处理)cur
4.先右后左(如果有),把该节点的子节点压入栈中
5.循环执行1->2->3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 package mainimport ( "errors" "fmt" ) type Node struct { Value int Left *Node Right *Node } type Stack struct { MaxTop int Top int Arr [7 ]*Node } func (s *Stack) Push (pushNode *Node) error if s.Top == s.MaxTop-1 { return errors.New("栈满了" ) } s.Top++ s.Arr[s.Top] = pushNode return nil } func (s *Stack) Pop () (popNode *Node, err error) if s.Top == -1 { return nil , errors.New("空栈" ) } popNode = s.Arr[s.Top] s.Arr[s.Top] = nil s.Top-- return popNode, nil } func (s *Stack) List () if s.Top == -1 { fmt.Println("空栈" ) } for i := 0 ; i < s.Top+1 ; i++ { fmt.Printf("Arr[%v]=%v\n" , i, s.Arr[i]) } } func ShowTree (head *Node) if head != nil { nodeStack := &Stack{MaxTop: 7 , Top: -1 } nodeStack.Push(head) for nodeStack.Top < nodeStack.MaxTop-1 && nodeStack.Top > -1 { tmpNode, _ := nodeStack.Pop() if tmpNode != nil { fmt.Println(tmpNode.Value) } if tmpNode.Right != nil { nodeStack.Push(tmpNode.Right) } if tmpNode.Left != nil { nodeStack.Push(tmpNode.Left) } } } } func main () root := &Node{Value: 1 } left := &Node{Value: 3 } right := &Node{Value: 4 } root.Left = left root.Right = right left1 := &Node{Value: 5 } right1 := &Node{Value: 6 } left2 := &Node{Value: 7 } right2 := &Node{Value: 8 } left.Left = left1 left.Right = right1 right.Left = left2 right.Right = right2 ShowTree(root) }
执行结果:
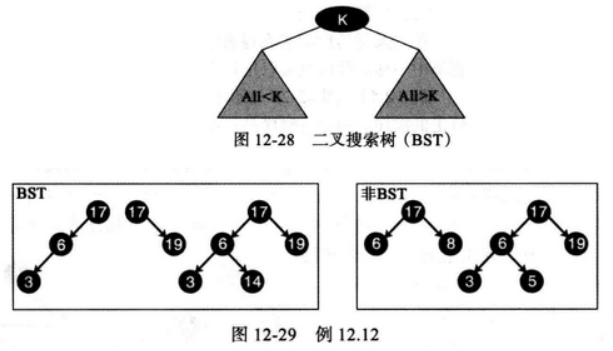
(6) 二叉搜索树的介绍 二叉搜索树(BST)是一种具有额外特性的二叉树:每个节点的关键字值大于左子树中的所有节点的关键字值,而小于右子树中所有节点的关键字值。
BST 一个非常有趣的特性是,一个是如果我们对二叉树应用中序遍历,被访问的元素以升序排列;而另一个有趣的特性是我们能对二叉搜索树使用在第8章中使用的折半査找。
例如,下图示了一些二叉搜索树和一些非二叉搜索树。当使用中序遍历时,得到列表:(3, 6, 17)、(17, 19)和(3, 6, 14, 17, 19).
weiyigeek.top-二叉搜索树
温馨提示: 如果所有子树是二叉搜索树,并且整棵树也是二叉搜索树,那这棵树才是二叉搜索树。
(7) 二叉搜索树的抽象数据类型 二叉树的抽象数据类型与我们为具有相同操作的广义线性表所定义的抽象数据类型相似。事实上,如今BST表比广义线性表更为常见,因为BST的査找效率比广义线性表要高,广义线性表中只能使用顺序査找,而BST中可以使用折半査找。
(8) 二叉搜索树的实现 同样,二叉搜索树(BST)可以使用数组或链表来实现,但是链表结构更为常见并且效率更高。
线性实现使用带有两个指针的节点左指针(左子树)和右指针(右子树),如果左子树为空,则左指针也为空;如果右子树为空,则右指针也为空;
像广义线性表的链表实现一样,BST的链表实现也使用一个与BST具有相同名字的虚构节点。该虚构节点的数据部分含有关于树的信息,如树中的节点数目,指针部分指向树的根。
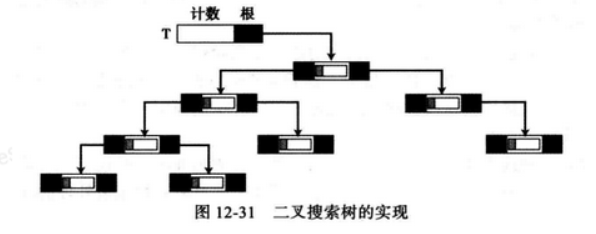
例如,下图显示了一棵二叉搜索树,其中每个节点的数据域是一个记录。
weiyigeek.top-二叉搜索树数据域
此处,仍然使用Go语言代码进行演示,编写二叉搜索树以及测试二叉搜索树。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 package main import ( "fmt" "sync" ) type TreeNode struct { key int value int leftNode *TreeNode rightNode *TreeNode } type BinarySearchTree struct { rootNode *TreeNode lock sync.RWMutex } func (tree *BinarySearchTree) InsertElement (key int , value int ) tree.lock.Lock() defer tree.lock.Unlock() var treeNode *TreeNode treeNode = &TreeNode{key, value, nil , nil } if tree.rootNode == nil { tree.rootNode = treeNode } else { insertTreeNode(tree.rootNode, treeNode) } } func insertTreeNode (rootNode *TreeNode, newTreeNode *TreeNode) if newTreeNode.key < rootNode.key { if rootNode.leftNode == nil { rootNode.leftNode = newTreeNode } else { insertTreeNode(rootNode.leftNode, newTreeNode) } } else { if rootNode.rightNode == nil { rootNode.rightNode = newTreeNode } else { insertTreeNode(rootNode.rightNode, newTreeNode) } } } func (tree *BinarySearchTree) PreOrderTraverseTree (function func (int ) ) tree.lock.Lock() defer tree.lock.Unlock() preOrderTraverseTree(tree.rootNode, function) } func preOrderTraverseTree (treeNode *TreeNode, function func (int ) ) if treeNode != nil { function(treeNode.value) preOrderTraverseTree(treeNode.leftNode, function) preOrderTraverseTree(treeNode.rightNode, function) } } func (tree *BinarySearchTree) InOrderTraverseTree (function func (int ) ) tree.lock.RLock() defer tree.lock.RUnlock() inOrderTraverseTree(tree.rootNode, function) } func inOrderTraverseTree (treeNode *TreeNode, function func (int ) ) if treeNode != nil { inOrderTraverseTree(treeNode.leftNode, function) function(treeNode.value) inOrderTraverseTree(treeNode.rightNode, function) } } func (tree *BinarySearchTree) PostOrderTraverseTree (function func (int ) ) tree.lock.Lock() defer tree.lock.Unlock() postOrderTraverseTree(tree.rootNode, function) } func postOrderTraverseTree (treeNode *TreeNode, function func (int ) ) if treeNode != nil { postOrderTraverseTree(treeNode.leftNode, function) postOrderTraverseTree(treeNode.rightNode, function) function(treeNode.value) } } func (tree *BinarySearchTree) MinNode () *int tree.lock.RLock() defer tree.lock.RUnlock() var treeNode *TreeNode treeNode = tree.rootNode if treeNode == nil { return (*int )(nil ) } for { if treeNode.leftNode == nil { return &treeNode.value } treeNode = treeNode.leftNode } } func (tree *BinarySearchTree) MaxNode () *int tree.lock.RLock() defer tree.lock.RUnlock() var treeNode *TreeNode treeNode = tree.rootNode if treeNode == nil { return (*int )(nil ) } for { if treeNode.rightNode == nil { return &treeNode.value } treeNode = treeNode.rightNode } } func (tree *BinarySearchTree) SearchNode (key int ) bool tree.lock.RLock() defer tree.lock.RUnlock() return searchNode(tree.rootNode, key) } func searchNode (treeNode *TreeNode, key int ) bool if treeNode == nil { return false } if key < treeNode.key { return searchNode(treeNode.leftNode, key) } if key > treeNode.key { return searchNode(treeNode.rightNode, key) } return true } func (tree *BinarySearchTree) RemoveNode (key int ) tree.lock.Lock() defer tree.lock.Unlock() removeNode(tree.rootNode, key) } func removeNode (treeNode *TreeNode, key int ) *TreeNode if treeNode == nil { return nil } if key < treeNode.key { treeNode.leftNode = removeNode(treeNode.leftNode, key) return treeNode } if key > treeNode.key { treeNode.rightNode = removeNode(treeNode.rightNode, key) return treeNode } if treeNode.leftNode == nil && treeNode.rightNode == nil { return nil } if treeNode.leftNode == nil { treeNode = treeNode.leftNode return treeNode } if treeNode.rightNode == nil { treeNode = treeNode.rightNode return treeNode } var leftmostrightNode = treeNode.rightNode for { if leftmostrightNode != nil && leftmostrightNode.leftNode != nil { leftmostrightNode = leftmostrightNode.leftNode } else { break } } treeNode.key, treeNode.value = leftmostrightNode.key, leftmostrightNode.value treeNode.rightNode = removeNode(treeNode.rightNode, treeNode.key) return treeNode } func (tree *BinarySearchTree) ShowTree () tree.lock.Lock() defer tree.lock.Unlock() fmt.Println("-----------------------------------------" ) stringify(tree.rootNode, 0 ) fmt.Println("-----------------------------------------" ) } func stringify (treeNode *TreeNode, level int ) if treeNode != nil { format := "" for i := 0 ; i < level; i++ { format += " " } format += "---[ " level++ stringify(treeNode.leftNode, level) fmt.Printf(format+"%d\n" , treeNode.key) stringify(treeNode.rightNode, level) } } func main () var tree *BinarySearchTree = &BinarySearchTree{} tree.InsertElement(8 , 8 ) tree.InsertElement(3 , 3 ) tree.InsertElement(10 , 10 ) tree.InsertElement(1 , 1 ) tree.InsertElement(6 , 6 ) tree.ShowTree() }
执行结果:1 2 3 4 5 6 7 ----------------------------------------- ---[ 1 ---[ 3 ---[ 6 ---[ 8 ---[ 10 -----------------------------------------
12.6 图 图是由一组节点(称为顶点)和一组顶点间的连线(称为边或弧)构成的一种抽象数据类型。
图与树的区别是什么?
树是定义成层次结构的,节点只能有一个双亲,而图中的节点可以有一个或多个双亲。
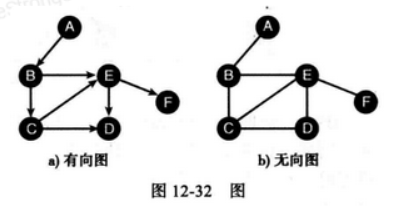
图可能是有向的或无向的,例如下图展示的。
在有向图中,连接两个顶点的边都有从一个顶点到另一个顶点的方向(在图中用箭头表示)。
在无向图中,边是没有方向的。
weiyigeek.top-有向图与无向图
图中的顶点可以代表对象或概念,边或弧可以代表这些对象或概念间的关系。如果图是有向的,那么关系就是单向的;如果图是无向的,那么关系就是双向的。
例如,城市的地图和连接城市的道路可以表示成计算机中的一个无向图。城市是顶点,无向边是连接它们的道路。如果我们要显示出城市间的距离,可以使用加权图,其中的每条边都有一个权重,该权重表示由这条边连接的两个城市间的距离。
例如,图的另一个应用是在计算机网络(第6章)中的应用。顶点可以代表节点或集线器,边可以代表路由。每条边都有一个权重,表示从一个集线器到相邻集线器的代价。路由器能使用图算法找到它与包最终目的地间的最短路径。